科目：czsx 来源：广东省实验中学2010届初中毕业班一模考试数学试题 题型：059
(1)如图，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．
①求证：BE＋CF＞EF.
②若∠A＝90°，探索线段BE、CF、EF之间的数量关系，并加以证明；
(2)如图，在四边形ABCD中，∠B＋∠C＝180°，DB＝DC，∠BDC＝120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．
科目：czsx 来源：2009年浙江省嵊州市普通高中提前招生考试数学试卷 题型：059
课外兴趣小组活动时，老师提出了如下问题：
如图，△ABC中，若AB＝5，AC＝3，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE＝AD，再连结BE(或将△ACD绕点D逆时针旋转180°得到△EBD)，把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．
感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．
(2)问题解决：
受到(1)的启发，请你证明下面命题：如图，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连结EF．
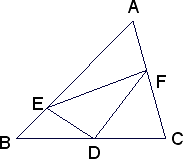
①求证：BE＋CF＞EF
②若∠A＝90°，探索线段BE、CF、EF之间的等量关系，并加以证明．
(3)问题拓展：
如图，在四边形ABDC中，∠B＋∠C＝180°，DB＝DC，∠BDC＝120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连结EF，探索线段BE、CF、EF之间的数量关系，并加以证明．
科目：czsx 来源：2013年吉林省长春市高级中等学校招生考试数学 题型：059
探究：如图①，在四边形ABCD中，∠BAD＝∠BCD＝90°，AB＝AD，AE⊥CD于点E．若AE＝10，求四边形ABCD的面积．
应用：如图②，在四边形ABCD中，∠ABC＋∠ADC＝180°，AB＝AD，AE⊥BC于点E．若AE＝19，BC＝10，CD＝6，则四边形ABCD的面积为________．
科目：czsx 来源：2008年浙江省湖州市初中毕业升学统一考试、数学试卷 题型：059
已知：在矩形AOBC中，OB＝4，OA＝3，分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边BC上的一个动点(不与B、C重合)，过F点的反比例函数y＝
(k＞0)的图象与AC边交于点E．
(1)求证：△AOE与△BOF的面积相等．
(2)记S＝S△OEF－S△ECF，求当k为何值时，S有最大值，最大值为多少？
(3)请探索：是否存在这样的点F，做一日和尚撞一天钟得将CEF沿EF对折后，C点恰好落在OB上？若存在，求出点F的坐标，若不存在，请说明理由．
科目：czsx 来源：2008年天津市初中毕业升学统一考试、数学试卷 题型：059
已知Rt△ABC中，∠ACB＝90°，CA＝CB，有一个圆心角为45°，半径的长等于CA的扇形CEF绕点C旋转，且直线CE，CF分别与直线AB交于点M，N．
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时，如图①，求证：MN2＝AM2＋BN2；
思路点拨：考虑MN2＝AM2＋BN2符合勾股定理的形式，需转化为在直角三角形中解决．可将△ACM沿直线CE对折，得△DCM，连DN，只需证DN＝BN，∠MDN＝90°就可以了．
请你完成证明过程：
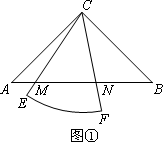
(Ⅱ)当扇形CEF绕点C旋转至图②的位置时，关系式MN2＝AM2＋BN2是否仍然成立？若成立，请证明；若不成立，请说明理由．
科目：czsx 来源：2009年黑龙江省牡丹江市初中毕业学业考试数学试题 题型：059
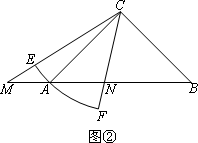
已知Rt△ABC中，AC＝BC，∠C＝90°，D为AB边的中点，∠EDF＝90°，∠EDF绕D点旋转，它的两边分别交AC、CB(或它们的延长线)于E、F．
当∠EDF绕D点旋转到DE⊥AC于E时(如图1)，易证
．
当∠EDF绕E点旋转到DE和AC不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，S△DEF、S△CEF、S△ABC又有怎样的数量关系？请写出你的猜想，不需证明．
科目：czsx 来源：2009年北京市朝阳区初三二模数学试题 题型：044
在△ABC中，点D在AC上，点E在BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转得到△
(使
＜180°)，连接
、
，设直线与AC交于点O．
(1)如图，当AC＝BC时，
的值为________；
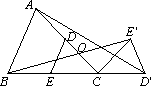
(2)如图，当AC＝5，BC＝4时，求的值；
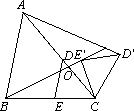
(3)在(2)的条件下，若∠ACB＝60°，且E为BC的中点，求△OAB面积的最小值．
科目：czsx 来源：辽宁省朝阳市2011年初中毕业升学考试数学试卷 题型：059
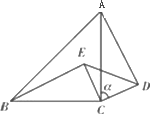
如图，在△ABC中，∠ACB＝90°，AC＝BC＝
，点D在AC上，点E在BC上，且CD＝CE，连接DE．
(1)线段BE与AD的数量关系是________，位置关系是________．
(2)如图，当△CDE绕点C顺时针旋转一定角度α后，(1)中的结论是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．
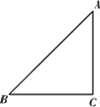
(3)绕点C继续顺时针旋转△CDE，当90°＜α＜180°时，延长DC交AB于点F，请在下图中补全图形，并求出当AF＝1＋
时，旋转角α的度数．
科目：czsx 来源：2008年辽宁省沈阳市初中毕业升学统一考试、数学试卷 题型：059
已知：如图①所示，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．
(1)求证：①BE＝CD；②△AMN是等腰三角形．
(2)在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出(1)中的两个结论是否仍然成立；
(3)在(2)的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．
科目：czsx 来源：安徽省2011年初中毕业学业考试数学试题 题型：059
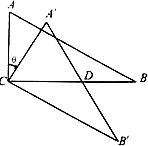
在△
ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为
(0°＜＜180°)，得到△
C．
(1)如图，当AB∥C
时，设AB与CB/相交于D．证明：△
CD是等边三角形；
(2)如图，连接A、
B，设△AC和△BC的面积分别为
和
．求证：∶＝1∶3；
(3)如图，设AC中点为E，B/中点为P，AC＝a，连接EP，当＝_________°时，EP长度最大，最大值为_________．
科目：czsx 来源：江苏省无锡市2010年数学中考试题 题型：059
(1)如图，在正方形ABCD中，M是BC边(不含端点B、C)上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN＝90°，求证：AM＝MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE＝MC，连ME．正方形ABCD中，∠B＝∠BCD＝90°，AB＝BC．∴∠NMC＝180°－∠AMN－∠AMB＝180°－∠B－∠AMB＝∠MAB＝∠MAE．
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图)，N是∠ACP的平分线上一点，则当∠
AMN＝60°时，结论AM＝MN是否还成立？请说明理由．
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X”，请你作出猜想：当∠AMN＝________°时，结论AM＝MN仍然成立．(直接写出答案，不需要证明)
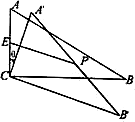
科目：czsx 来源：2009年辽宁省沈阳市中考数学试题 题型：059
将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F．
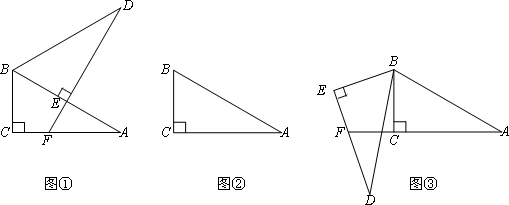
(1)求证：AF＋EF＝DE；
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其他条件不变，请在图②中画出变换后的图形，并直接写出(1)中的结论是否仍然成立；
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其他条件不变，如图③．你认为(1)中的结论还成立吗？若成立，写出证明过程；若不成立，请写出此时AF、EF与DE之间的关系，并说明理由．
科目：czsx 来源：江苏省徐州市2007年初中毕业、升学考试数学试题 题型：044
如图，△ABC中，点D在AC上，点E在BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转得到△C
(使∠BC＜180°)，连接A、B设直线B与AC、A分别交于点O、E．
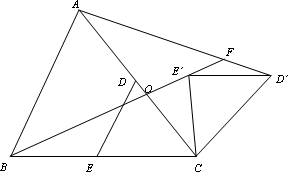
(1)若△ABC为等边三角形，则
的值为________，∠AFB的度数为________，(2)若△ABC满足∠ACB＝60°，AC＝
，BC＝
，
①求的值和∠AFB的度数
②若E为BC的中点，求△OBC面积的最大值．
科目：czsx 来源：2006年初中数学总复习下册 题型：059
已知：如图，△ABC中，点D、E分别在边AB、AC上，连结DE并延长交BC的延长线于点F，连结DC、BE．若∠BDE＋∠BCE＝180°．
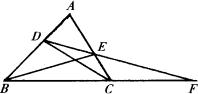
(1)写出图中三对相似三角形(注意：不得添加字母和线)
(2)请在你所找出的相似三角形中选取一对，说明它们相似的理由．
科目：czsx 来源：2011年辽宁省锦州市初中生学业考试数学试卷 题型：059
如图(1)～(3)，已知∠AOB的平分线OM上有一点P，∠CPD的两边与射线OA、OB交于点C、D，连接CD交OP于点G，设∠AOB＝α(0°＜α＜180°)，∠CPD＝β．
(1)如图(1)，当α＝β＝90°时，试猜想PC与PD，∠PDC与∠AOB的数量关系(不用说明理由)；
(2)如图(2)，当α＝60°，β＝120°时，(1)中的两个猜想还成立吗？请说明理由．
(3)如图(3)，当α＋β＝180°时，①你认为(1)中的两个猜想是否仍然成立，若成立请直接写出结论；若不成立，请说明理由．
②若
＝2，求
的值．
科目：czsx 来源：河北省石家庄市42中2010届初三毕业班第二次模拟考试数学试题 题型：059
如图，在直角梯形ABCD中，AD∥BC，∠B＝∠A＝90°，AD＝a，BC＝b，AB＝c．
操作示例
我们可以取直角梯形ABCD的腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC拼接到△PFD的位置，构成新图形．(如图1)
思考发现
小敏在操作后发现，该剪拼方法就是将△PEC绕点P逆时针旋转180°到△PED的位置，易知PE与PF在同一直线上，又因为在梯形ABCD中，AD∥BC，∠C＋∠ADP＝180°，则∠FDP＋∠ADP＝180°，所以AD和DF在同一直线上，那么构成的新图形是一个四边形，而且进一步可证得，该四边形是一个特殊的平行四边形——矩形．
实践探究
(1)矩形ABEF的面积是________．(用含a、b、c的式子表示)
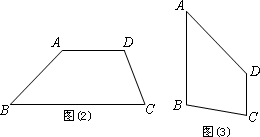
(2)类比图(1)的剪接办法，请你就图(2)和图(3)中的两种情形分别画出剪拼成一个平行四边形的示意图．(注：图(2)和图(3)中的四边形均为梯形)
解决问题
小明原来有一块七巧板，形状为平行四边形ACDE，如图(4)所示，不小心损坏了一条边变成了五边形ABCDE的形状如图(5)所示，小明现在打算将图(5)中五边形在不改变其面积的前提下通过裁剪与拼接变成一个平行四边形，请你帮他画出剪接的示意图，并说明理由．
科目：czsx 来源：2008年北京市朝阳区初三一模数学试卷(一) 题型：059
如图，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，则有结论EF＝BE＋FD成立；
(1)如图，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是BC、CD上的点，且∠EAF是∠BAD的一半，那么结论EF＝BE＋FD是否仍然成立？若成立，请证明；若不成立，请说明理由；
(2)若将(1)中的条件改为：在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，延长BC到点E，延长CD到点F，使得∠EAF仍然是∠BAD的一半，则结论EF＝BE＋FD是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．
科目：czsx 来源：北京市昌平区2011年中考一模数学试题 题型：059
已知，点P是∠MON的平分线上的一动点，射线PA交射线OM于点A，将射线PA绕点P逆时针旋转交射线ON于点B，且使∠APB＋∠MON＝180°．
(1)利用图1，求证：PA＝PB；
(2)如图2，若点C是AB与OP的交点，当S△POB＝3S△PCB时，求PB与PC的比值；
(3)若∠MON＝60°，OB＝2，射线AP交ON于点D，且满足且∠PBD＝∠ABO，请借助图3补全图形，并求OP的长．
科目：czsx 来源：2011年江苏省苏州市中考模拟（二）数学卷 题型：选择题
如图，在菱形ABCD中，∠B＝60°，点E、F分别从点B、D出发，以同样的速度沿边BC、DC向点C运动．下列四个结论：①AE＝AF；②∠CEF＝∠CFE；③当E、F分别是边BC、DC的中点时，EF＝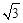
BE；④当E、F分别是边BC、DC的中点时，△AEF的面积最大，其中，正确的有 ( )
A．①②③ B．①②④ C．①③④ D．②③④
