练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >长方形abcd的边ab=4cm,bc=2cm,若动点p从点A出发,在折线AD-DC-CB上以1cm/s的速度匀

    长方形abcd的边ab=4cm,bc=2cm,若动点p从点A出发,在折线AD-DC-CB上以1cm/s的速度匀答案解析

    科目：gzsx 来源： 题型：

    已知矩形ABCD的边AB=4cm，BC=3cm，如图所示，矩形的顶点A，B为某一椭圆的两个焦点，且椭圆经过矩形的另外两个顶点C，D，试建立适当的坐标系，求椭圆的方程．

    查看答案和解析>>

    科目：gzsx 来源：2008-2009学年福建省福州市高二（上）模块数学试卷（选修2-1）（解析版） 题型：解答题

    已知矩形ABCD的边AB=4cm，BC=3cm，如图所示，矩形的顶点A，B为某一椭圆的两个焦点，且椭圆经过矩形的另外两个顶点C，D，试建立适当的坐标系，求椭圆的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    4、在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点，如果EF与HG交于点M，那么（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    平行四边形ABCD的边AB和BC所在的直线方程分别是x+y-1=0、3x-y+4=0，对角线的交点是O（3，3）．
    （1）求边CD所在直线的方程；
    （2）平行四边形ABCD的面积．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，M、N、P分别为空间四边形ABCD的边AB，BC，CD上的点，且AM：MB=CN：NB=CP：PD．
    求证：（1）AC∥平面MNP，BD∥平面MNP；
    （2）平面MNP与平面ACD的交线∥AC．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    点E、F、G、H分别是四面体ABCD的边AB、BC、CD、DA的中点，则四面体的六条棱中与平面EFGH平行的条数是（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在空间四边形ABCD的边AB，BC，CD，DA上分别取E，F，G，H使
    AE
    EB
    =
    AH
    HD
    =1，
    CF
    FB
    =
    CG
    GD
    =
    1
    2
    ，则（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

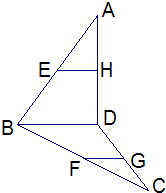
    精英家教网已知E，F，G，H为空间四边形ABCD的边AB，BC，CD，DA的中点，BD，AC所成角为60°．且BD=a，AC=b，求四边形EFGH的面积．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    点E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点，且BD=AC，则四边形EFGH是
    菱形
    菱形
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

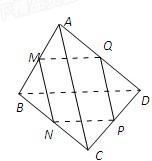
    精英家教网如图，已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点．
    求证：（1）线段MP和NQ相交且互相平分；
    （2）AC∥平面MNP，BD∥平面MNP．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知E、F、G、H分别是空间四边形ABCD的边AB，BC，CD，DA的中点．
    （1）证明E，F，G，H四点共面；
    （2）证明BD∥平面EFGH．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

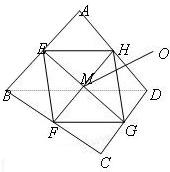
    精英家教网已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点．
    （1）用向量法证明E，F，G，H（2）四点共面；
    （2）用向量法证明：BD∥平面EFGH；
    （3）设M是EG和FH的交点，求证：对空间任一点O，有
    OM
    =
    1
    4
    (
    OA
    +
    OB
    +
    OC
    +
    OD
    )    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

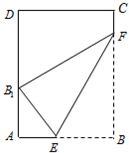
    精英家教网如图，矩形纸片ABCD的边AB=24，AD=25，点E、F分别在边AB与BC上．现将纸片的右下角沿EF翻折，使得顶点B翻折后的新位置B1恰好落在边AD上．设
    BEEF
    =t    ，EF=l，l关于t的函数为l=f（t），试求：
    （1）函数f（t）的解析式；
    （2）函数f（t）的定义域．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    20、已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点，且EH∥FG．
    求证：EH∥BD．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    点 E，F，G，H分别为空间四边形ABCD的边AB，BC，CD，AD的中点，则四边形EFGH是（　　）
    A、菱形B、梯形C、正方形D、平行四边形

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，则AC与平面EFGH的位置关系是
    平行
    平行
    ．

    查看答案和解析>>

    科目：gzsx 来源：2012年人教A版高中数学必修二2.2直线、平面平行的判定及其性质练习卷（二） 题型：解答题

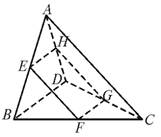
    如图，□EFGH的四个顶点分别在空间四边形ABCD的边AB、BC、CD、DA上，求证：BD∥面EFGH，AC∥面EFGH．

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF与HG交于点M,则…(    )

    A.M一定在直线AC上

    B.M一定在直线BD上

    C.M可能在AC上,也可能在BD上

    D.M不在AC上,也不在BD上

    查看答案和解析>>

    科目：gzsx 来源：2013届山东省临沂市高二上学期期末质量检测调研理科数学 题型：解答题

    ．（本小题满分12分）如图所示，矩形ABCD的边AB=，BC=2，PA⊥平面ABCD，PA=2，现有数据： ①；②；③；建立适当的空间直角坐标系，

    （I）当BC边上存在点Q，使PQ⊥QD时，可能取所给数据中的哪些值?请说明理由；

    （II）在满足（I）的条件下，若取所给数据的最小值时，这样的点Q有几个? 若沿BC方向依次记为，试求二面角的大小.

     

     

     

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.

    (1)用向量法证明E、F、G、H四点共面；

    (2)用向量法证明:　BD∥平面EFGH；

    (3)设M是EG和FH的交点，

    求证:对空间任一点O，有.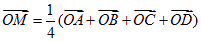

    查看答案和解析>>