已知函数f(x)=Acos(ωx+θ)的图像如图K20-1所示答案解析
科目:gzsx
来源:
题型:
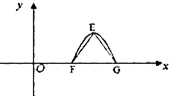
(2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
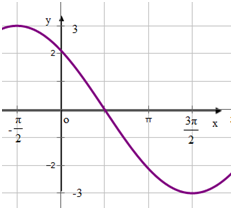
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示则f(x)的函数解析式为( )
| |
| |
查看答案和解析>>
科目:gzsx
来源:
题型:
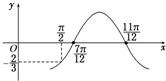
已知函数f(x)=Acos(ωx+φ)的图象如图所示,f(
)=-
,则f(0)=
.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2013•浙江)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ=
”的( )
查看答案和解析>>
科目:gzsx
来源:
题型:
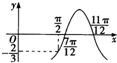
已知函数f(x)=Acos(ωx+φ)的图象如图所示,f(
)=-
,则f(0)=( )
查看答案和解析>>
科目:gzsx
来源:
题型:
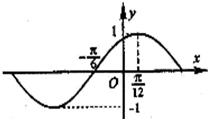
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<
,x∈R)的图象的一部分如下图所示.
(1)求函数f(x)的解析式;
(2)当x∈[-
,]时,求函数y=f(x)+f(x+
)的最大值与最小值及相应的x的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
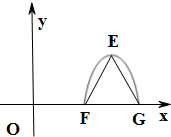
已知函数f(x)=Acos(ωx+α)(A>0,ω>0,0<α<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
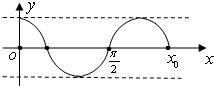
已知函数f(x)=Acos(ωx+φ),在x=0处取得最大值,并过点
(,0),(x0,0).它的图象如下图,则x
0的值是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=Acos(
+),x∈R,且f(
)=
.
(1)求A的值;
(2)设α,β∈[0,
],f(4a+
π)=
-,f(4
β-π)=
,求cos(α+β)的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=sinωx+acosωx(a>0,ω>0)的图象关于直线x=
对称,点(
,0)是函数图象的一个对称中心,则a+ω的最小值是
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=
asinωx-acosωx
(a>0,ω>0)的图象上两相邻最高点与最低点的坐标分别为(
,2),(
-,-2).
(Ⅰ)求a与ω的值;
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且f(A)=2,求
的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)在区间
[x0,x0+]上单调递减,则函数g(x)=Acos(ωx+φ)在同一区间上为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
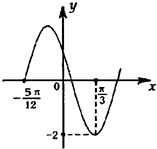
(2011•焦作一模)已知函数f(x)的图象过点(
,-
),它的导函数f′(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其中A>0,ω>0,|φ|<
,为了得到函
数f(x)的图象,只要将函数y=sinx(x∈R)的图象上所有的点( )
|
|
|
|
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=sin(2x+φ)+acos(2x+φ),其中a,φ为正常数,且0<φ<π,若f(x)的图象关于直线
x=对称,f(x)的最大值为2.
(1)求a和φ的值;
(2)由y=f(x)的图象经过怎样的平移得到
y=2sin(2x+)的图象.
查看答案和解析>>
科目:gzsx
来源:
题型:
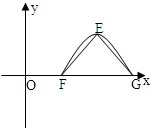
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
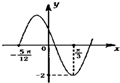
已知函数f(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其A>0,ω>0,|φ|<
,为了得到函f(x)的图象,只要将函数g(x)=2cos
2-2sin
2(x∈R)的图象上所有的点( )
|
|
|
|
查看答案和解析>>
科目:gzsx
来源:
题型:
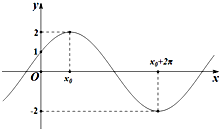
(2013•普陀区二模)已知函数f(x)=Acos(ωx+ϕ)(A>0,ω>0,
-<ϕ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x
0,2)和(x
0+2π,-2)
(1)求函数f(x)的解析式;
(2)若锐角θ满足
cosθ=,求f(2θ)的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<
) 的图象过点(0,
),最小正周期为
,且最小值为-1.
(1)求函数f(x)的解析式.
(2)若x∈[
,m],f(x)的值域是[-1,-
],求m的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=
Acos(+),x∈R,且
f()=,则A=
2
2
.
查看答案和解析>>
科目:gzsx
来源:2011年河南省焦作市高考数学一模试卷(理科)(解析版)
题型:选择题
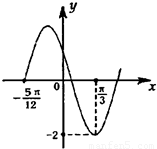
已知函数f(x)的图象过点(
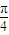
,-

),它的导函数f′(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其中A>0,ω>0,|φ|<

,为了得到函
数f(x)的图象,只要将函数y=sinx(x∈R)的图象上所有的点( )
A.向左平移

个单位长度,再把所得各点的横坐标缩短到原来的

倍,纵坐标不变,最后沿y轴方向向下平移一个单位长度
B.向左平移

个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,最后沿y轴方向向上平移一个单位长度
C.向左平移
个单位长度,再把得所各点的横坐标缩短到原来的

倍,纵坐标不变,最后沿y轴方向向下平移一个单位长度
D.向左平移
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,最后沿y轴方向向上平移一个单位长度
查看答案和解析>>

 (2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( )
(2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( ) 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|< 已知函数f(x)=Acos(ωx+α)(A>0,ω>0,0<α<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为
已知函数f(x)=Acos(ωx+α)(A>0,ω>0,0<α<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为 已知函数f(x)=Acos(ωx+φ),在x=0处取得最大值,并过点(
已知函数f(x)=Acos(ωx+φ),在x=0处取得最大值,并过点( (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点( 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( ) 已知函数f(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其A>0,ω>0,|φ|<
已知函数f(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其A>0,ω>0,|φ|< (2013•普陀区二模)已知函数f(x)=Acos(ωx+ϕ)(A>0,ω>0,-
(2013•普陀区二模)已知函数f(x)=Acos(ωx+ϕ)(A>0,ω>0,- ,-
,- ),它的导函数f′(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其中A>0,ω>0,|φ|<
),它的导函数f′(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其中A>0,ω>0,|φ|< ,为了得到函
,为了得到函
 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变,最后沿y轴方向向下平移一个单位长度
倍,纵坐标不变,最后沿y轴方向向下平移一个单位长度 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,最后沿y轴方向向上平移一个单位长度
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,最后沿y轴方向向上平移一个单位长度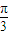 个单位长度,再把得所各点的横坐标缩短到原来的
个单位长度,再把得所各点的横坐标缩短到原来的 倍,纵坐标不变,最后沿y轴方向向下平移一个单位长度
倍,纵坐标不变,最后沿y轴方向向下平移一个单位长度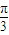 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,最后沿y轴方向向上平移一个单位长度
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,最后沿y轴方向向上平移一个单位长度