
科目:gzsx 来源: 题型:
| x2+8 | ||
|
| x2+8 | ||
|
| x2+4+4 | ||
|
(
| ||
|
| x2+4 |
| 4 | ||
|
| x2+1+c | ||
|
| 1+c | ||
|
科目:gzsx 来源:2011年江苏省高考数学权威预测试卷(2)(解析版) 题型:解答题
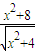 的最值时,我们可以将
的最值时,我们可以将 化成
化成 ,再将分式分解成
,再将分式分解成 ,然后利用基本不等式求最值;借此,计算使得
,然后利用基本不等式求最值;借此,计算使得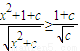 对一切实数x都成立的正实数c的范围是 .
对一切实数x都成立的正实数c的范围是 . 科目:gzsx 来源: 题型:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 8 |
| 2 |
| 5+1 |
| 2 |
科目:gzsx 来源: 题型:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 6 |
| 2 |
| 9+1 |
| 2 |
科目:gzsx 来源: 题型:
 某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.
某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.| 3 | 16 |
科目:gzsx 来源: 题型:
(2009•普宁市模拟)为了确保神州七号飞船发射时的信息安全,信息须加密传输,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
|
科目:gzsx 来源: 题型:
| p |
| q |
| 3 |
| 4 |
| 1 |
| 7 |
| 3 |
| 8 |
| 4 |
| 7 |
| 9 |
| 16 |
科目:gzsx 来源: 题型:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 8 |
| 2 |
科目:gzsx 来源: 题型:

|
| 8 |
| 2 |
| 5+1 |
| 2 |
| A、lhho | B、eovl |
| C、ohhl | D、love |
科目:gzsx 来源: 题型:
| a | b | c | d | e | f | g | h | i | J | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 8 |
| 2 |
| 25+1 |
| 2 |
科目:gzsx 来源: 题型:
 |
| 1≤i≤j≤n |
 |
| 1≤i≤j≤n |
| S1 |
| S2 |
| S2 |
| S3 |
| Sn |
| Sn+1 |
| n |
| 4 |
| 3 |
| 16 |
| 3 |
| 16 |
| 1 |
| 2n |
科目:gzsx 来源: 题型:
| p |
| q |
| 3 |
| 4 |
| p |
| q |
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| n |
| A、1 | B、2 | C、3 | D、4 |