练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >y=5-2 z=5-25

    y=5-2 z=5-25答案解析

    科目：gzsx 来源： 题型：单选题

    若点A(2，1，4)与点P(x，y，z)的距离为5，则下列关系式正确的是


    1. A.
      (x-2)2+(y-1)2+(z-4)2＝25
    2. B.
      (x-2)2+(y-1)2+(z-4)2＝5
    3. C.
      (x+2)2+(y+1)2+(z+4)2＝25
    4. D.
      (x+2)2+(y+1)2+(z-4)2＝25

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    某医院一天派出医生下乡医疗，派出医生人数及其概率如下：

    医生人数

    0

    1

    2

    3

    4

    5人及以上

    概率

    0.1

    0.16

    x

    y

    0.2

    z

     (1)若派出医生不超过2人的概率为0.56，求x的值；

    (2)若派出医生最多4人的概率为0.96，最少3人的概率为0.44，求y、z的值.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

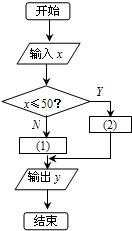    11、铁路托运行李，从甲地到乙地，按规定每张客票托运行李不超过50kg时，每千克0.2元，超过50kg时，超过部分按每千克0.25元计算，某同学画出了计算行李价格的算法框图（如图所示），则在程序框图中（1）应填的内容是
    y=0.2×50+0.25×（x-50）
    ，（2）应填的内容是
    y=0.2×x
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    点P（x，y，z）满足
    		(x-1)2+(y-1)2+(z+1)2
    =2，则点P在（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若x,y 满足条件求下列各式的最大值与最小值：

    (1)z=2x+y；(2)z=2x-3y.

    查看答案和解析>>

    科目：gzsx 来源：训练必修五数学苏教版 苏教版 题型：044

    若x，y满足条件求下列各式的最大值与最小值．

    (1)Z＝2x＋y；(2)Z＝2x－3y．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：单选题

    点P（x，y，z）满足
    		(x-1)2+(y-1)2+(z+1)2
    =2，则点P在（　　）
    A．以点（1，1，-1）为圆心，以2为半径的圆上
    B．以点（1，1，-1）为中心，以2为棱长的正方体上
    C．以点（1，1，-1）为球心，以2为半径的球面上
    D．无法确定

    查看答案和解析>>

    科目：gzsx 来源：训练必修五数学人教A版 人教A版 题型：044

    若x，y满足条件求下列各式的最大值与最小值：

    (1)z＝2x＋y；

    (2)z＝2x－3y．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    我们把球外一点与球面上一动点之间距离的最小值,叫做该点到球面的距离.如果等比数列{an}的首项a1为空间一点(t,1,2)到球面(x+8)2+(y-4)2+(z+2)2=16的距离,Sn为数列{an}的前n项和,且Sn=2,则等比数列{an}的公比q等于

    A.1                   B.                     C.                    D.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2007•咸安区模拟）设z=2x+y，实数x、y满足不等式组
    x≥1
    3x+5y≤25
    △
    y≥2
    y≥2
    ，若当且仅当x=5，y=2时，z取得最大值，则不等式组中应增加的不等式可以是
    y≥2
    y≥2
    ．（只要写出适合条件的一个不等式即可）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知两实数x，y满足
    x-y+2≥0
    x+y-4≥0
    2x-y-5≤0

    求：（1）z=3x-2y的最大值；
    （2）z=x2+y2-10y+25的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知
    x-y+2≥0
    x+y-4≥0
    2x-y-5≤0
    求：
    （Ⅰ）z=x2+y2-10y+25的最小值；
    （Ⅱ）z=
    y+1
    x+1
    的范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点Pn（an，bn）都在直线l：y=2x+2上，P1为直线l与x轴的交点，数列{an}成等差数列，公差为1（n∈N*）．
    （I）求数列{an}，{bn}的通项公式；
    （Ⅱ）若f（n）=
    an(n=2m+1)
    bn(n=2m)
    （m∈Z），问是否存在k∈N*，使得f（k+5）=2f（k）-2成立？若存在，求出k的值，若不存在，说明理由；
    （Ⅲ）求证：
    1
    |P1P2|2
    +
    1
    |P1P3|2
    +…+
    1
    |P1Pn|2
    ＜
    2
    5
    （n≥2，n∈N*）．

    查看答案和解析>>

    科目：gzsx 来源： 题型：013

    设复数z=x+yi(x，y∈R)且|z-2|=又|z-3|=4，那|z|是

    [    ]

    A．25　　　B．5　　C．1　　D．7

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料
    日期 3月1日 3月2日 3月3日 3月4日 3月5日
    温差x（°C） 10 11 13 12 8
    发芽数y（颗） 23 25 30 26 16
    （I）从3月1日至3月5日中任选2天，记发芽的种子数分别为m，n，求事件“m，n均小于25”的概率．
    （II）请根据3月2日至3月4日的数据，求出y关于x的线性回归方程
    y
    =
    b
    x+
    a
    ；
    （III）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（II）所得的线性回归方程是否可靠？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设实数x，y满足
    x-y+5≥0
    x+y≥0
    x≤3
    ，则z=x+3y的最小值为（　　）
    A、-6B、-3C、5D、2

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2009•红桥区二模）若P（-2，1）为圆（x+1）2+y2=25的弦AB的中点，则直线AB的方程是（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了5月1日至5月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料：
    日    期 5月1日 5月2日 5月3日 5月4日 5月5日
    温差x（°C） 10 12 11 13 8
    发芽数y（颗） 23 25 30 26 16
    （1）从5月1日至5月5日中任选2天，记发芽的种子数分别为m，n，求事件“m，n均不小于25”的概率．
    （2）根据5月2日至5月4日的数据，利用相关系数r判断y与x是否具有线性相关关系（参考数据：|r|＞0.75时，认为两变量有很强的线性相关；
    		7
    =2.6458    ）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•滨州一模）设实数x，y满足约束条件
    x-y+2≥0
    x+y-4≥0
    2x-y-5≤0
    ，则目标函数z=x+2y的最大值为
    25
    25
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•德州一模）已知在平面直角坐标系xOy上的区域D由不等式组
    x+y-5≤0
    y≥x
    x≥1
    确定，若M（x，y）为区域D上的动点，点A的坐标为（2，3），则z=
    OA
    •
    OM
    的最大值为（　　）

    查看答案和解析>>