精英家教网 >
试题搜索列表 >已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.答案解析
科目:czsx
来源:
题型:
(2013•和平区二模)已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(Ⅰ)如图①,若⊙O的半径为5,求线段OC的长;
(Ⅱ)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求
的值.

查看答案和解析>>
科目:czsx
来源:
题型:
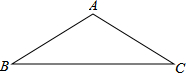
如图,已知△ABC中,AB=AC,∠BAC=120°,求AB:BC的值.
查看答案和解析>>
科目:czsx
来源:
题型:
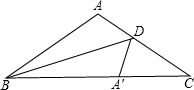
已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD:DC=
.
查看答案和解析>>
科目:czsx
来源:
题型:

10、如图,已知△ABC中,AB=AC,D、E分别在BC、AC上,且AD=AE.则∠1与∠2的关系是( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC=
12
12
cm.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
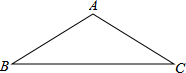 如图,已知△ABC中,AB=AC,∠BAC=120°,求AB:BC的值.
如图,已知△ABC中,AB=AC,∠BAC=120°,求AB:BC的值.
查看答案和解析>>
科目:czsx
来源:2006年上海市宝山区中考数学二模试卷(解析版)
题型:填空题
已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD:DC=
.

查看答案和解析>>
科目:czsx
来源:2006年江苏省常州市新桥中学中考数学模拟试卷(二)(解析版)
题型:填空题
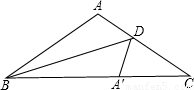
已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD:DC=
.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD:DC=________.
已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD:DC=________.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
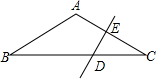 如图,已知△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC=________cm.
如图,已知△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC=________cm.
查看答案和解析>>
科目:czsx
来源:期中题
题型:单选题
如图,已知△ABC中,AB=AC,D、E分别在BC、AC上,且AD=AE. 则∠1与∠2的关系是
A、2∠1=∠2
B、2∠2=∠1
C、∠1=∠2
D、∠B=∠1+∠2
查看答案和解析>>
科目:czsx
来源:上海期末题
题型:填空题
已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD∶DC=( )。
查看答案和解析>>
科目:czsx
来源:
题型:单选题
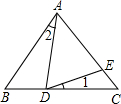 如图,已知△ABC中,AB=AC,D、E分别在BC、AC上,且AD=AE.则∠1与∠2的关系是
如图,已知△ABC中,AB=AC,D、E分别在BC、AC上,且AD=AE.则∠1与∠2的关系是
- A.
2∠1=∠2
- B.
2∠2=∠1
- C.
∠1=∠2
- D.
∠B=∠1+∠2
查看答案和解析>>
科目:czsx
来源:
题型:
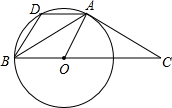
(2012•常德)如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D,
求证:(1)AC是⊙O的切线;
(2)四边形BOAD是菱形.
查看答案和解析>>
科目:czsx
来源:
题型:
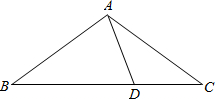
如图,△ABC中,AB=AC,∠BAC=108°,在BC边上取一点D,使BD=BA,连接AD.
求证:
(1)△ADC∽△BAC;
(2)点D是BC的黄金分割点.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D,
如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D,
求证:(1)AC是⊙O的切线;
(2)四边形BOAD是菱形.
查看答案和解析>>
科目:czsx
来源:
题型:

24、已知△ABC中,AB=AC,点O是高AD上一点,⊙O与AB相切于E,求证:⊙O与AC相切.
查看答案和解析>>
科目:czsx
来源:
题型:
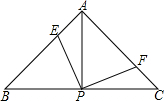
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下五个结论:
①AE=CF;②∠APE=∠CPF;③△EFP是等腰直角三角形;④EF=BE+CF;⑤S
四边形=
S
△ABC 其中正确结论的编号是
①②③⑤
①②③⑤
.
查看答案和解析>>
科目:czsx
来源:
题型:
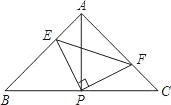
如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:
①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤S
四边形AEPF=
S
△ABC.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有
.
查看答案和解析>>
科目:czsx
来源:
题型:
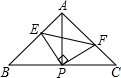
如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,给出以下四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③S
四边形AEPF=
S
△ABC;
④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的有( )
查看答案和解析>>




 已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD:DC=________.
已知△ABC中,AB=AC,∠BAC=120°,点D是边AC上一点,连BD,若沿直线BD翻折,点A恰好落在边BC上,则AD:DC=________.

 如图,已知△ABC中,AB=AC,D、E分别在BC、AC上,且AD=AE.则∠1与∠2的关系是
如图,已知△ABC中,AB=AC,D、E分别在BC、AC上,且AD=AE.则∠1与∠2的关系是 (2012•常德)如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D,
(2012•常德)如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D, 如图,△ABC中,AB=AC,∠BAC=108°,在BC边上取一点D,使BD=BA,连接AD.
如图,△ABC中,AB=AC,∠BAC=108°,在BC边上取一点D,使BD=BA,连接AD. 如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D,
如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D, 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下五个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下五个结论: 如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:
如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论: 如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,给出以下四个结论:
如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,给出以下四个结论: