
题目列表(包括答案和解析)
5.(理)已知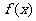 是
是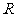 上的增函数,点
上的增函数,点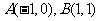 在它的图象上,
在它的图象上,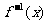 是它的反函数,则不等式
是它的反函数,则不等式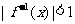 的解集为
的解集为
A.(0,1) B.(-1,0) C.(-1,1) D.(1,2)
(文)“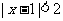 成立”是“
成立”是“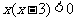 成立”的
成立”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知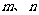 是两条不同的直线,
是两条不同的直线,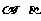 是两个不同的平面,且
是两个不同的平面,且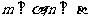 ,则下列命题中不正确的是
,则下列命题中不正确的是
A.若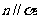 则
则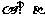 B.若
B.若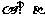 则
则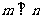
C.若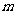 与
与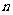 相交,则
相交,则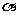 与
与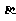 也相交 D.若
也相交 D.若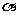 与
与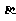 相交,则
相交,则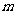 与
与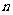 也相交
也相交
3.已知两个正数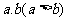 的等差中项是5,等比中项是4,则椭圆
的等差中项是5,等比中项是4,则椭圆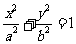 的离心率
的离心率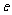 等于
等于
A.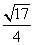 B.
B.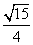 C.
C.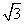 D.
D.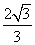
2.函数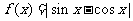 的最小正周期为
的最小正周期为
A.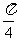 B.
B.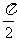 C.
C.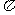 D.
D.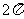
1.(理)若复数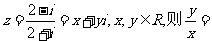
A.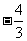 B.
B.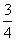 C.
C.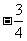 D.
D.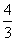
(文)若集合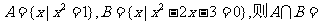
A.{ 3 }
B.{ 1 }
C.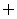 D.{ -1 }
D.{ -1 }
22.(本题满分14分)
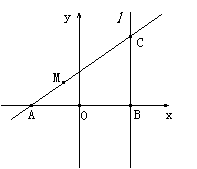 (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线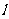 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与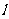 交于点C,点M在线段AC上,满足=.
交于点C,点M在线段AC上,满足=.
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 的直线与轨迹M交于
点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为
锐角三角形时t的取值范围.
22.(本题满分14分)
(理)已知数列{an}的前n项和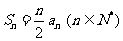 ,且
,且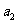 =1,
=1,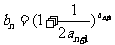
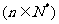 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1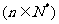 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
21.(文)已知:函数f(x)=a+ (a>1)
(1) 证明:函数f(x)在(-1,+∞ )上为增函数;
(2)证明方程f(x)=0没有负根.
21.(理)如图,|AB|=2,O为AB中点,直线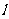 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与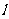 交于点C,点M在线段AC上,满足=.
交于点C,点M在线段AC上,满足=.
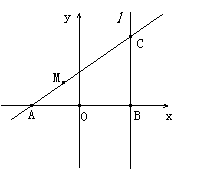 (1)求点M的轨迹方程;
(1)求点M的轨迹方程;
(2)若过B点且斜率为- 的直线与轨迹M交于
点P,点Q(t,0)是x轴上任意一点,求当
ΔBPQ为锐角三角形时t的取值范围.
20.某汽车销售公司为促销采取了较灵活的付款方式,对购买10万元一辆的轿车在一年
内将款全部付清的前提下,可以选择以下两种分期付款方案购车:
方案1:分3次付清,购买后4个月第一次付款,再过4个月第二次付款,再过4个月第三次付款.方案2:分12次付清,购买后1个月第一次付款,再过1个月第二次付款,……购买后12个月第十二次付款.
现规定分期付款中,每期付款额相同,月利率为0.8%,每月利息按复利计息,试比较以上两种方案的哪一种方案付款总数较少?(参考数据:1.0083=1.024,1.0084=1.033,1.00811=1.092,1.00812=1.1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com