20.设函数f(x)=x²-mlnx,h(x)=x²-x+a.

(1)　　　　　　　　　 当a=0时，f(x)≥h(x)在(1,+∞)上恒成立，求实数m的取值范围;

(2)　　　　　　　　　 当m=2时，若函数k(x)=f(x)-h(x)在［1,3］上恰有两个不同零点，求实数 a的取值范围;

(3)　　　　　　　　　 是否存在实数m，使函数f(x)和函数h(x)在公共定义域上具有相同的单调性？若存在，求出m的值，若不存在，说明理由。

19. 过点P(1，0)作曲线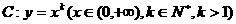的切线，切点为M₁，设M₁在x轴上的投影是点P₁。又过点P₁作曲线C的切线，切点为M₂，设M₂在x轴上的投影是点P₂，…。依此下去，得到一系列点M₁，M₂…，M_n，…，设它们的横坐标a₁，a₂，…，a_n，…，构成数列为。

　 (1)求证数列是等比数列，并求其通项公式；

　 (2)求证：；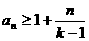

　 (3)当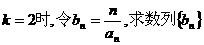的前n项和S_n。

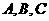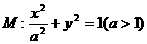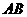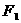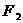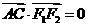18. 已知均在椭圆上，直线、分别过椭圆的左右焦点、，当时，有.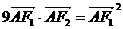

(Ⅰ)求椭圆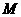的方程;

(Ⅱ)设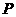是椭圆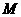上的任一点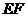，为圆的任一条直径，求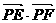的最大值.

17. 某高级中学共有学生2000人，各年级男、女生人数如下表：

已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.19.

(Ⅰ)现用分层抽样的方法在全校抽取48名学生，问应在高三年级抽取多少人？

(Ⅱ)已知求高三年级女生比男生多的概率.

16. 如图，在长方体ABCD－A₁B₁C₁D₁中，AB=AD=1,AA₁=2,

G是CC₁上的动点。

(Ⅰ)求证：平面ADG⊥平面CDD₁C₁

(Ⅱ)判断B₁C₁与平面ADG的位置关系，并给出证明；

15. 设函数。

　 (1)写出函数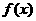的最小正周期及单调递减区间；

　 (2)当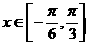时，函数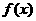的最大值与最小值的和为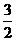，求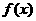的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积。

14．如果一条直线和一个平面垂直，则称此直线与平面构成一个“正交线面对”，在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成“正交线面对”的概率为________

13．已知函数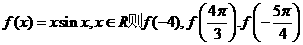的大小关系为_____________

12．若关于的不等式组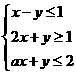表示的平面区域是一个三角形，则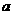的取值范围是_______________

11．设双曲线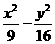=1的右顶点为，右焦点为，过点作平行双曲线的一条渐近线的直线与双曲线交于点，则的面积为___________