
题目列表(包括答案和解析)
4.
由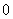 ,
,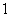 ,
,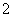 ,
,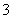 ,
,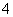 ,
,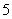 六个数字组成无重复数字且数字
六个数字组成无重复数字且数字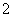 ,
,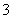 相邻的四位数共_______个(结果用数字表示).
相邻的四位数共_______个(结果用数字表示).
3.
已知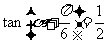 ,
,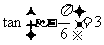 ,则
,则 ____________.
____________.
2.
若复数 满足
满足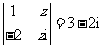 (
(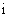 是虚数单位),则
是虚数单位),则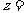 __________.
__________.
1.
若 ,则
,则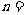 _____________.
_____________.
18.(本小题满分20分)
和平面解析几何的观点相同,在空间中,空间曲面可以看作是适合某种条件的动点的轨迹.一般来说,在空间直角坐标系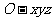 中,空间曲面的方程是一个三元方程
中,空间曲面的方程是一个三元方程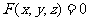 .
.
(Ⅰ)在直角坐标系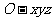 中,求到定点
中,求到定点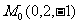 的距离为3的动点
的距离为3的动点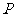 的轨迹(球面)方程;
的轨迹(球面)方程;
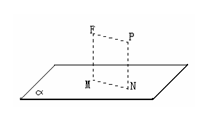
(Ⅱ)如图3,设空间有一定点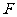 到一定平面
到一定平面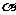 的距离为常数
的距离为常数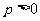 ,即
,即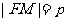 ,定义曲面
,定义曲面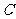 为到定点
为到定点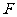 与到定平面
与到定平面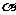 的距离相等(
的距离相等(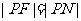 )的动点
)的动点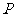 的轨迹,试建立适当的空间直角坐标系
的轨迹,试建立适当的空间直角坐标系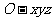 ,求曲面
,求曲面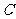 的方程;
的方程;
 (Ⅲ)请类比平面解析几何中对二次曲线的研究,讨论曲面
(Ⅲ)请类比平面解析几何中对二次曲线的研究,讨论曲面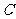 的几何性质.并在图4中通过画出曲面
的几何性质.并在图4中通过画出曲面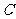 与各坐标平面的交线(如果存在)或与坐标平面平行的平面的交线(如果必要)表示曲面
与各坐标平面的交线(如果存在)或与坐标平面平行的平面的交线(如果必要)表示曲面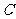 的大致图形.画交线时,请用虚线表示被曲面
的大致图形.画交线时,请用虚线表示被曲面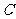 自身遮挡部分.
自身遮挡部分.
图3
17. (本小题满分20分)
(本小题满分20分)
将数列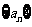 中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
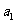
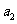
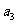
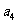
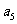
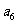
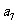
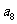
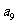
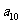
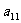
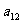
……
记表中的第一列数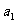 ,
,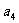 ,
,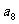 ,… ,构成数列
,… ,构成数列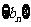 .
.
(Ⅰ)设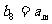 ,求
,求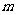 的值;
的值;
(Ⅱ)若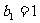 ,对于任何
,对于任何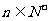 ,都有
,都有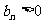 ,且
,且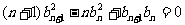 .求数列
.求数列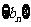 的通项公式;
的通项公式;
(Ⅲ)对于(Ⅱ)中的数列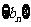 ,若上表中每一行的数按从左到右的顺序均构成公比为
,若上表中每一行的数按从左到右的顺序均构成公比为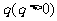 的等比数列,且
的等比数列,且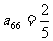 ,求上表中第
,求上表中第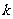 (
(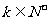 )行所有项的和
)行所有项的和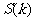 .
.
16. (本小题满分16分)
(本小题满分16分)
设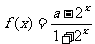 ,其中实常数
,其中实常数 .
.
(Ⅰ)求函数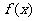 的定义域和值域;
的定义域和值域;
(Ⅱ)试研究函数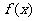 的基本性质,并证明你的结论.
的基本性质,并证明你的结论.
 14.(本小题满分14分)
14.(本小题满分14分)
如图2,在四棱锥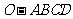 中,底面
中,底面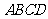 是边长为2的正方形,
是边长为2的正方形, ,
,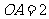 ,
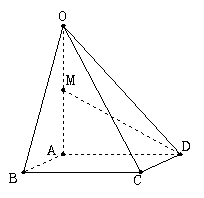
,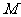 为
为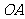 的中点.
的中点.
 (Ⅰ)求异面直线OC与MD所成角的大小;
(Ⅰ)求异面直线OC与MD所成角的大小;
(Ⅱ)求点M到平面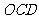 的距离.
的距离.
15. (本小题满分15分)
(本小题满分15分)
一种填数字彩票2元一张,购买者在卡上依次填上0~9中的两个数字(允许重复).中奖规则如下:
如果购买者所填的两个数字依次与开奖的两个有序数字分别对应相等,则中一等奖10元;
如果购买者所填的两个数字中,只有第二个数字与开奖的第二个数字相等,则中二等奖2元;
其他情况均无奖金.
(Ⅰ)小明和小辉在没有商量的情况下各买一张这种彩票,求他俩都中一等奖的概率;
(Ⅱ)设“购买一张这种彩票中一等奖”为事件A,“购买一张这种彩票中二等奖”为事件B,请指出事件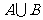 的含义,并求事件
的含义,并求事件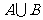 发生的概率;
发生的概率;
(Ⅲ)设购买一张这种彩票的收益为随机变量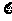 ,求
,求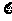 的数学期望.
的数学期望.
13.在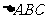 中,设
中,设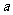 、
、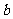 、
、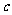 分别是
分别是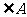 、
、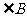 、
、 所对的边长,且满足条件
所对的边长,且满足条件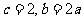 ,则
,则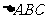 面积的最大值为………………………………………………………………… ( )
面积的最大值为………………………………………………………………… ( )
A.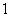 B.
B.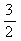 C.
C.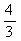 D.
D.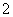
12.过点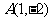 ,且与向量
,且与向量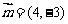 平行的直线的方程是…………………………( )
平行的直线的方程是…………………………( )
A.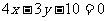 B.
B.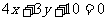 C.
C.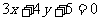 D.
D.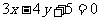
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com