
题目列表(包括答案和解析)
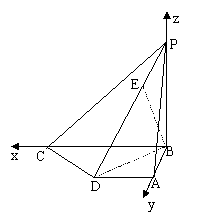
18、解法一:如图,以B为原点,分别以BC、BA、BP为x,y、z轴,建立空间直角坐标系,则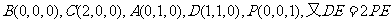
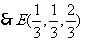
(1)
 ………4分
………4分
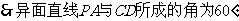 .
.
(2)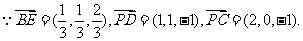
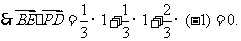
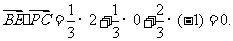
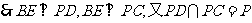 .
. 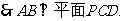
(3)设平面PAD的一个法向量为 .
.
令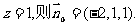
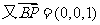 ,设平面PBD的法向量为
,设平面PBD的法向量为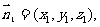
 令
令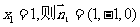
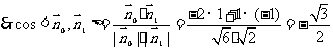
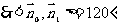
又二面角A-PD-B为锐二面角,故二面角A-PD-B的大小为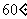 .
.
17、解:(1)由已知得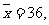 所以估计这年苹果的总产量为
所以估计这年苹果的总产量为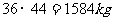 .
.
该农户卖苹果的收入将达7920元.(2)131/243;(3)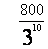
16. 解:由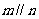 及A+B+C=
及A+B+C=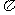 ,得
,得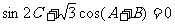 ,……………………(2分)
,……………………(2分)
即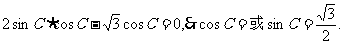 ………………………(4分)
………………………(4分)
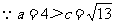 ,
,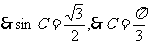 .………………………………………(6分)
.………………………………………(6分)
由余弦定理,得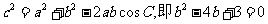 ,解得
,解得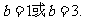 (9分)
(9分)
当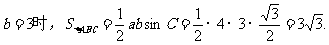
当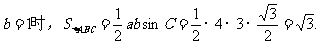 …………………………(12分)
…………………………(12分)
9、(-2,-1) 10、 y=x+1 11、-242 12、1/2 13、 (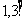 14、
14、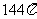 15、
15、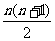
3900
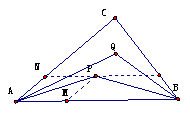
8、[解析]如图2,设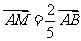 ,
,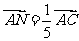 ,则
,则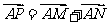 .由平行四边形法则,知NP∥AB,所以
.由平行四边形法则,知NP∥AB,所以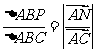 =
=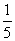 ,同理可得
,同理可得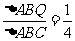 .故
.故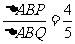 ,选B.
,选B.
21.( 13分)已知函数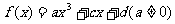 是R上的奇函数,当
是R上的奇函数,当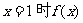 取得极值-2;
取得极值-2;
(1)求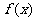 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意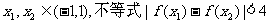 恒成立.
恒成立.
衡阳市八中2009届高三第九次月考数学(文)试题(090529)
BDCB ACCB
20、(13分)已知直线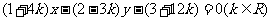 所经过的定点
所经过的定点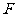 恰好是椭圆
恰好是椭圆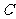 的一个焦点,且椭圆
的一个焦点,且椭圆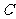 上的点到点
上的点到点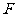 的最大距离为8.
的最大距离为8.
(1)求椭圆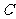 的标准方程;(5分)
的标准方程;(5分)
(2)已知圆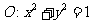 ,直线
,直线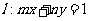 .试证明当点
.试证明当点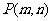 在椭圆
在椭圆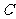 上运动时,直线
上运动时,直线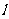 与圆
与圆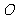 恒相交;并求直线
恒相交;并求直线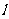 被圆
被圆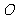 所截得的弦长的取值范围. (8分)
所截得的弦长的取值范围. (8分)
19、(13分)在等差数列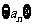 中,公差
中,公差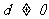 ,且
,且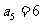 ,
(1)求
,
(1)求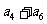 的值.
的值.
(2)当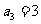 时,在数列
时,在数列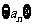 中是否存在一项
中是否存在一项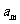 (
(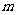 正整数),使得
正整数),使得 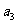 ,
,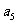 ,
,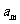 成等比数列,若存在,求
成等比数列,若存在,求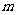 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)若自然数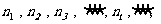 (
(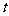 为正整数)
为正整数)
满足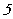 <
< 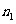 <
<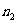 <
<
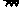 <
< 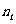 <
<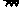 ,
使得
,
使得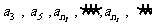 成等比数列,
成等比数列,
当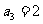 时, 用
时, 用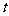 表示
表示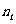 .
.
18、(12分)已知如图四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
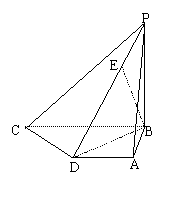 (1)求异面直线PA与CD所成的角的大小;
(1)求异面直线PA与CD所成的角的大小;
(2)求证:BE⊥平面PCD;
(3)求二面角A-PD-B的大小.
17、(12分)李大爷种了44株苹果树,收获时先随意采摘5株果树上的苹果,称得每株果树上苹果重量如下(单位;kg): 35 , 35 , 34 , 39 , 37. 技术人员按品质将这批苹果分为A、B、C三类,其比例为2:3:1(假设苹果大小、质量、色泽相似)。李大爷把这些苹果送到集市上去卖,顾客甲、乙各任购5个苹果 。
(1) 根据样本平均数,估计这年苹果的总产量为多少? 若市场上苹果售价为每千克5元,则李大爷卖苹果的收入将达多少元?
(2) 求甲买的苹果中至少有2个A类苹果的概率;
(3)
若甲、乙购买的苹果中各有m,n个A类苹果,则求 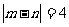 时的概率。
时的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com