
题目列表(包括答案和解析)
20. 已知函数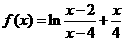 .
.
(I)求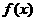 的极值;
的极值;
(II)求证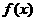 的图象是中心对称图形;
的图象是中心对称图形;
(III)设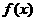 的定义域为
的定义域为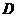 ,是否存在
,是否存在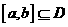 .当
.当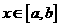 时,
时,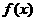 的取值范围是
的取值范围是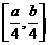 ?若存在,求实数
?若存在,求实数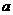 、
、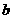 的值;若不存在,说明理由.
的值;若不存在,说明理由.
19. 有一幅椭圆型彗星轨道图,长4cm,高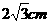 ,如下图,已知O为椭圆中心,A1,A2是长轴两端点,太阳位于椭圆的左焦点F处.
,如下图,已知O为椭圆中心,A1,A2是长轴两端点,太阳位于椭圆的左焦点F处.
(Ⅰ)建立适当的坐标系,写出椭圆方程,并求出当彗星运行到太阳正上方时二者在图上的距离;
 (Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,设P是l上异于D点的任意一点,直线A1P,A2P分别交椭圆于M、N(不同于A1,A2)两点,问点A2能否在以MN为直径的圆上?试说明理由.
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,设P是l上异于D点的任意一点,直线A1P,A2P分别交椭圆于M、N(不同于A1,A2)两点,问点A2能否在以MN为直径的圆上?试说明理由.
.
18. 已知函数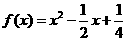 ,
,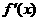 为函数
为函数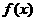 的导函数.
的导函数.
(1)若数列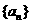 满足:
满足: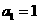 ,
,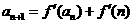 (
(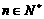 ) 求数列
) 求数列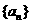 的通项
的通项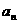 ;
;
(2)若数列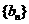 满足:
满足: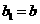 ,
,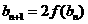 (
(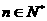 ).
).
①当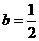 时,数列
时,数列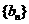 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列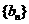 的通项
的通项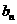 ;若不是,请说明理由;
;若不是,请说明理由;
②当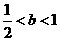 时,求证:
时,求证: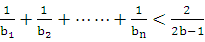
17. 某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值)
(3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
16.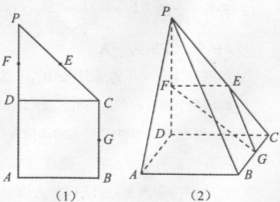 如图(1)在直角体型
如图(1)在直角体型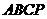 中,
中,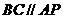 ,
,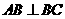 ,
,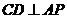 ,
,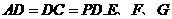 分别是
分别是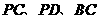 的中点,现将
的中点,现将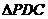 沿
沿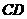 折起,使平面
折起,使平面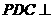 平面
平面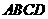 (如图2),且所得到的四棱锥
(如图2),且所得到的四棱锥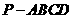 的正视图、侧视图、俯视图的面积总和为8。
的正视图、侧视图、俯视图的面积总和为8。
(1)求证: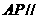 平面
平面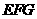 ;
;
(2)在线段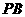 上确定一点
上确定一点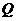 ,使
,使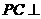 平面
平面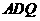 ,并给出证明过程。
,并给出证明过程。
15. 已知函数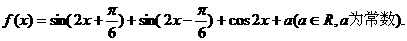
(I)求函数的最小正周期;
(II)求函数的单调递减区间;
(III)若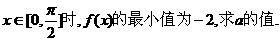
14.设函数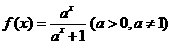 ,
,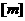 表示不超过实数m的最大整数,则函数
表示不超过实数m的最大整数,则函数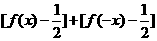 的值域是 .
的值域是 .
13.已知点A、B、C、D在同一球面上,AB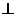 平面
平面 ,
,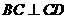 ,若
,若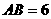 ,
,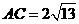 ,
,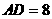 ,则B、C两点间的球面距离是 .
,则B、C两点间的球面距离是 .
12. 已知正数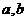 满足
满足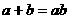 ,则
,则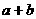 的最小值为
;
的最小值为
;
11. 一个几何体的三视图如右图所示,则该几何体外接球的表面积为 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com