
题目列表(包括答案和解析)
28.(命题人:海门中学陈达,审题人:海门中学方伟)
结论:圆C: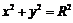 与x轴相交于M、N两点,设点P是圆C上任一点,则直线PM、PN斜率的乘积是定值.
与x轴相交于M、N两点,设点P是圆C上任一点,则直线PM、PN斜率的乘积是定值.
(1)写出以上结论在椭圆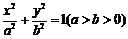 中的推广,并加以证明;
中的推广,并加以证明;
(2)将(1)的结论类比到双曲线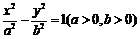 ,并加以证明.
,并加以证明.
解:(1)设椭圆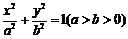 与x轴交于M、N两点,设点P是椭圆上任一点,则直线PM、PN斜率的乘积是定值.
与x轴交于M、N两点,设点P是椭圆上任一点,则直线PM、PN斜率的乘积是定值.
证明:由题意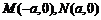 ,设
,设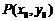 ,
,
则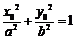 ,所以
,所以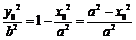 ,所以
,所以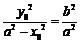 .
.
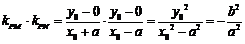 是定值.
是定值.
(2)设双曲线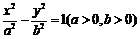 与x轴交于M、N两点,设点P是双曲线上任一点,则直线PM、PN斜率的乘积是定值.
与x轴交于M、N两点,设点P是双曲线上任一点,则直线PM、PN斜率的乘积是定值.
证明:由题意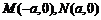 ,设
,设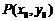 ,
,
则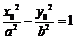 ,所以
,所以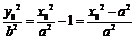 ,所以
,所以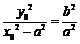 .
.
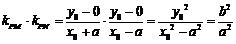 是定值.
是定值.
27.(命题人:海门中学周裕冲,审题人:海门中学方伟)
已知函数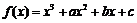 在点P
在点P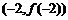 处的切线方程为
处的切线方程为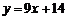 ,又
,又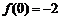 .
.
(1)求函数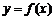 的解析式;
的解析式;
(2)求函数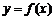 的单调区间和极值;
的单调区间和极值;
(3)若函数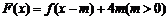 在区间
在区间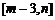 上的值域为
上的值域为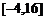 ,求
,求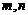 应满足的条件.
应满足的条件.
解:(1)由题设,知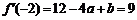 ,
,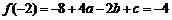 ,
,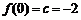 ,
,
解得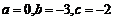 ,所以
,所以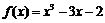 .
.
(2)由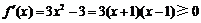 ,得
,得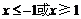 .由
.由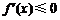 ,得
,得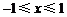 .
.
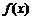 的单调增区间是
的单调增区间是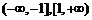 ,单调减区间为
,单调减区间为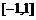 .
.
当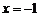 时,
时,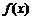 取得极大值0,当
取得极大值0,当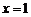 时,
时,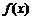 取得极小值
取得极小值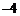 .
.
(3)由(2)知,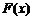 在
在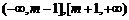 上是增函数,在
上是增函数,在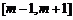 上是减函数.因为
上是减函数.因为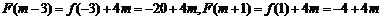 ,
,
所以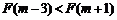 ,所以
,所以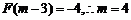 .
.
此时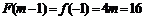 ,由
,由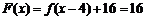 ,得
,得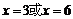 .
.
所以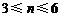 .
.
综上,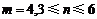 .
.
26.(命题人:海门中学方伟,审题人:海门中学沈永飞)
解不等式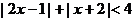 .
.
解:(Ⅰ)当x<-2时,得-(2x-1)-(x+2)<4,得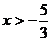 ,此不等式无解.
,此不等式无解.
(Ⅱ)当-2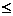 x<
x<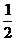 ,得-(2x-1)+(x+2)<4,得x>-1,
,得-(2x-1)+(x+2)<4,得x>-1,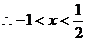 .
.
(Ⅲ)当x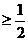 时,得(2x-1)+(x+2)<4,得
时,得(2x-1)+(x+2)<4,得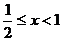 .
.
综上,原不等式的解集为(-1,1).
25.(命题人:通州中学薛国均,审题人:通州中学宋茂华.改编)
已知圆O的方程为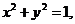 过直线
过直线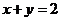 上的任意一点P作圆O的切线PA、PB.四边形OABP的面积取得最小时的点P的坐标(m,n)设
上的任意一点P作圆O的切线PA、PB.四边形OABP的面积取得最小时的点P的坐标(m,n)设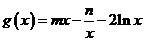 .
.
(1)求证:当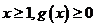 恒成立;
恒成立;
(2)讨论关于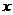 的方程:
的方程: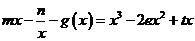 根的个数.
根的个数.
解析:(1)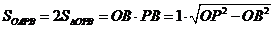 =
=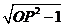 .
.
当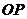 取得最小值时
取得最小值时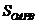 取得最小,过点O 作
取得最小,过点O 作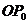 垂直于直线
垂直于直线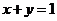 ,交点为
,交点为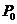 ,
,
易得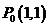 ,∴
,∴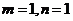 .∴
.∴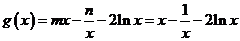 .
.
∴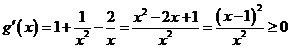 ,∴
,∴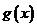 在
在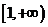 是单调增函数,
是单调增函数,
∴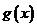
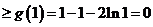 对于
对于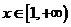 恒成立.
恒成立.
(2)方程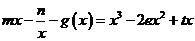 ,∴
,∴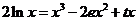 .
.
∵ 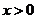 ,∴ 方程为
,∴ 方程为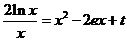 .令
.令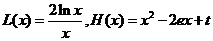 ,
,
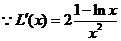 ,当
,当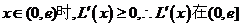 上为增函数;
上为增函数;
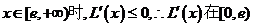 上为减函数,
上为减函数,
当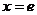 时,
时,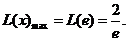
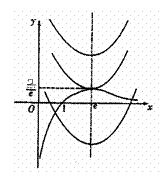
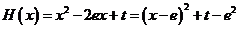 ,
,
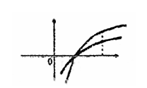
∴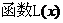 、
、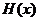 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
∴①当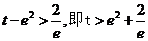 时,方程无解.
时,方程无解.
②当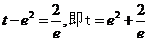 时,方程有一个根.
时,方程有一个根.
③当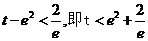 时,方程有两个根.
时,方程有两个根.
24.(命题人:通州中学薛国均,审题人:通州中学宋茂华.改编)
已知数列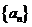 满足
满足 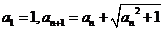 ,令
,令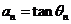
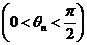 ,求证
,求证
(1)数列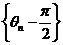 是等比数列;
是等比数列;
(2)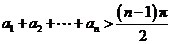 .
.
解析:(1)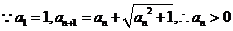 .
.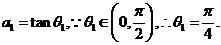
∴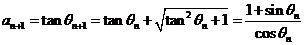 =
=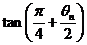 ,
,
∵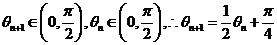 ,∴
,∴ 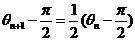 .
.
∴数列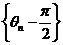 是等比数列.
是等比数列.
(2)∵ 数列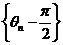 是等比数列,∴
是等比数列,∴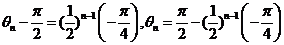 .
.
∵ 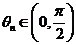 ,∴
,∴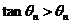 ,∴
,∴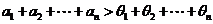 .
.
∵ 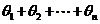 =
=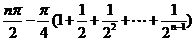
=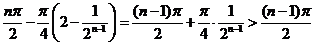 ,
,
∴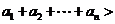
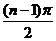 .
.
23.(命题人:如东中学何鹏,审题人:如东中学缪林,由2008年广东省韶关市高三摸底考试数学(理)第21题改编.)
设函数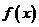 的定义域为R,当x<0时
的定义域为R,当x<0时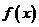 >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有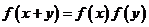 .
.
(Ⅰ)求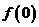 ,判断并证明函数
,判断并证明函数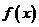 的单调性;
的单调性;
(Ⅱ)数列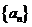 满足
满足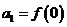 ,且
,且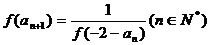 .
.
①求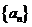 通项公式.
通项公式.
②当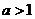 时,不等式
时,不等式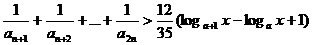 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.
[解析](Ⅰ)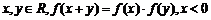 时,f(x)>1.
时,f(x)>1.
令x=-1,y=0,则f(-1)=f(-1)f(0).∵f(-1)>1 ,∴f(0)=1.
若x>0,则f(x-x)=f(0)=f(x)f(-x).
故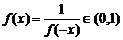 ,故x∈R, f(x)>0.
,故x∈R, f(x)>0.
任取x1<x2,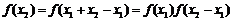 ,
,
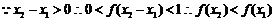 ,故f(x)在R上减函数.
,故f(x)在R上减函数.
(Ⅱ)①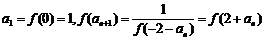 .由f(x)单调性,an+1=an+2 ,
.由f(x)单调性,an+1=an+2 ,
故{an}等差数列,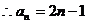 .
.
②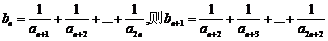 .
.
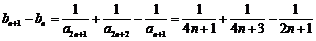
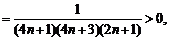
∴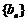 是递增数列.
是递增数列.
 当n≥2时,
当n≥2时,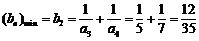 ,
,
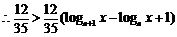 ,
,
即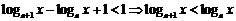 .
.
而a>1,∴x>1,故x的取值范围(1,+∞).
22.(命题人:如东中学葛张勇 ,审题人:如东中学何鹏,由《中学数学教学参考》2008年第1期题目改编 )
有红色和黑色两个盒子,红色盒中有6张卡片,其中一张标有数字0,2张标有数字1,3张标有数字2;黑色盒中有7张卡片,其中4张标有数字0,1张标有数字1,2张标有数字2.现从红色盒中任意取1张卡片(每张卡片被抽出的可能性相等),黑色盒中任取2张卡片(每张卡片被抽出的可能性相等),共取3张卡片.
(Ⅰ)求取出的3张卡片都标有数字0的概率;
(Ⅱ)求取出的3张卡片数字之积是4的概率;
(Ⅲ)求取出的3张卡片数字之积是0的概率.
[解析](Ⅰ)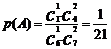 ;(Ⅱ)
;(Ⅱ)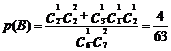 ;
;
(Ⅲ)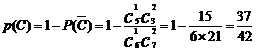 .
.
答:(略).
21. (选题人:启东中学徐建明,审题人:启东中学李俊)
设A(x1,y1),B(x2,y2)是函数f(x)=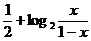 的图象上任意两点,且
的图象上任意两点,且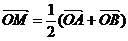 ,已知点M的横坐标为
,已知点M的横坐标为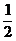 .
.
(1)求证:M点的纵坐标为定值;
(2)若Sn=f(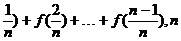 ∈N*,且n≥2,求Sn.
∈N*,且n≥2,求Sn.
(3)已知an=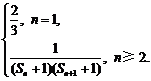 其中n∈N*.
其中n∈N*.
Tn为数列{an}的前n项和,若Tn<λ(Sn+1+1)对一切n∈N*都成立,试求λ的取值范围.
[解析](1)证明:∵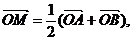 ∴M是AB的中点.设M点的坐标为(x,y),
∴M是AB的中点.设M点的坐标为(x,y),
由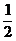 (x1+x2)=x=
(x1+x2)=x=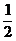 ,得x1+x2=1,则x1=1-x2或x2=1-x1.
,得x1+x2=1,则x1=1-x2或x2=1-x1.
而y=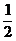 (y1+y2)=
(y1+y2)= 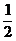 [f(x1)+f(x2)] =
[f(x1)+f(x2)] =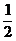 (
(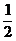 +log2
+log2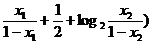
=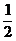 (1+log2
(1+log2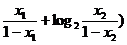 =
=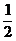 (1+log2
(1+log2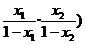
=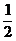 (1+log2
(1+log2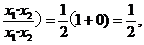 ∴M点的纵坐标为定值
∴M点的纵坐标为定值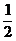 .
.
(2)由(1),知x1+x2=1,f(x1)+f(x2)=y1+y2=1,
Sn=f(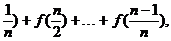 Sn=f(
Sn=f(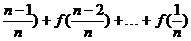 ,
,
两式相加,得
2Sn=[f(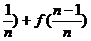 )+[f(
)+[f(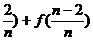 )+…+[f(
)+…+[f(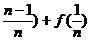 )
)
=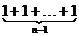 ,∴Sn=
,∴Sn=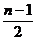 (n≥2,n∈N*).
(n≥2,n∈N*).
(3)当n≥2时,an=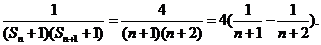
Tn=a1+a2+a3+…+an=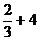 [(
[(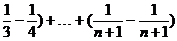 ]
]
=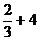 (
(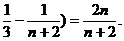
由Tn<λ(Sn+1+1),得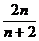 <λ·
<λ·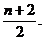 ∴λ>
∴λ>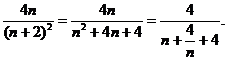
∵n+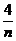 ≥4,当且仅当n=2时等号成立,∴
≥4,当且仅当n=2时等号成立,∴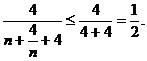
因此λ>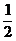 ,即λ的取值范围是(
,即λ的取值范围是(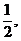 +∞).
+∞).
20. (选题人:启东中学陈兵,审题人:启东中学李俊)
已知定理:“若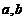 为常数,
为常数,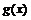 满足
满足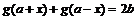 ,则函数
,则函数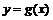 的图象关于点
的图象关于点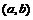 中心对称”.设函数
中心对称”.设函数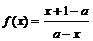 ,定义域为A.
,定义域为A.
(1)试证明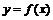 的图象关于点
的图象关于点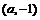 成中心对称;
成中心对称;
(2)当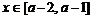 时,求证:
时,求证: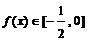 ;
;
(3)对于给定的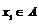 ,设计构造过程:
,设计构造过程: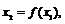
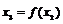 ,…,
,…,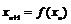 .如果
.如果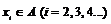 ,构造过程将继续下去;如果
,构造过程将继续下去;如果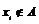 ,构造过程将停止.若对任意
,构造过程将停止.若对任意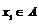 ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.
[解析](1)∵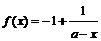 ,∴
,∴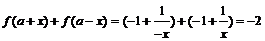 .
.
由已知定理,得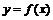 的图象关于点
的图象关于点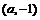 成中心对称.
成中心对称.
(2)先证明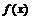 在
在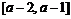 上是增函数,只要证明
上是增函数,只要证明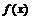 在
在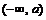 上是增函数.
上是增函数.
设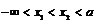 ,则
,则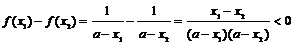 ,
,
∴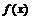 在
在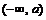 上是增函数.
上是增函数.
再由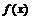 在
在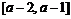 上是增函数,得
上是增函数,得
当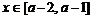 时,
时,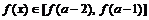 ,即
,即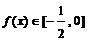 .
.
(3)∵构造过程可以无限进行下去,∴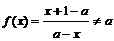 对任意
对任意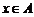 恒成立.
恒成立.
∴方程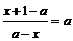 无解,即方程
无解,即方程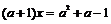 无解或有唯一解
无解或有唯一解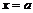 .
.
∴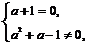 或
或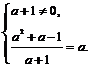 由此得到
由此得到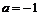 .
.
19. (选题人:启东中学陈高峰,审题人:启东中学李俊)
已知函数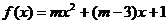 的图象x轴的交点至少有一个在原点右侧.
的图象x轴的交点至少有一个在原点右侧.
(1)求实数m的取值范围;
(2)令t=-m+2,求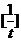 的值(其中[t]表示不大于t的最大整数);
的值(其中[t]表示不大于t的最大整数);
(3)对(2)中的t,求函数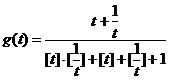 的值域.
的值域.
[解析]若m=0 则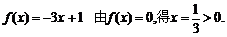 符合题意.
符合题意.
若m≠0 ,①m<0时,∵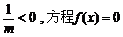 两根异号,∴必有一个负根.
两根异号,∴必有一个负根.
②m>0时,由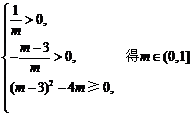 时,方程有两正根.综上得
时,方程有两正根.综上得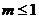 .
.
(2)∵t=-m+2 ,∴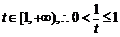 .当t=1时,
.当t=1时,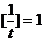 ,当t>1时,
,当t>1时,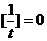 .
.
(3)当t=1时,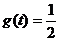 ;当t>1时,
;当t>1时,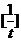 =0,设[t]=n,且t=[t]+a,则
=0,设[t]=n,且t=[t]+a,则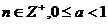 .
.
于是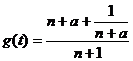 .由函数
.由函数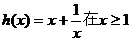 时是增函数,
时是增函数,
及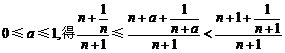 .
.
设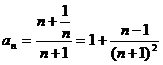 递减,∴
递减,∴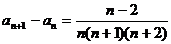 .
.
∴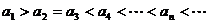 .
.
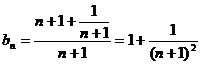 递减,∴
递减,∴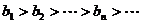 .
.
于是t>1时,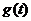 的值域为
的值域为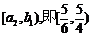 .
.
综上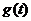 的值域为
的值域为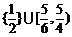 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com