
题目列表(包括答案和解析)
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知集合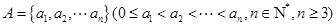 具有性质
具有性质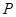 :对任意
:对任意 ,
,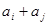 与
与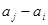 至少一个属于
至少一个属于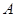 .
.
(1)分别判断集合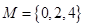 与
与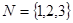 是否具有性质
是否具有性质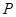 ,并说明理由;
,并说明理由;
(2)①求证: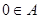 ;
;
②求证: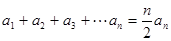 ;
;
(3)研究当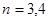 和
和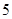 时,集合
时,集合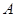 中的数列
中的数列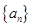 是否一定成等差数列.
是否一定成等差数列.
(本小题满分18分)过直线![]() 上的点
上的点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,联结
,联结![]() (1)当点
(1)当点![]() 在直线
在直线![]() 上运动时,证明:直线
上运动时,证明:直线![]() 恒过定点
恒过定点![]() ;
;
(2)当![]() ∥
∥![]() 时,定点
时,定点![]() 平分线段
平分线段![]()
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知函数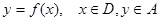 ;
;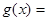
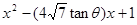 ,
,
(1)当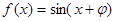 为偶函数时,求
为偶函数时,求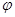 的值。
的值。
(2)当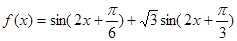 时,
时,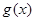 在
在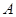 上是单调递增函数,求
上是单调递增函数,求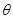 的取值范围。
的取值范围。
(3)当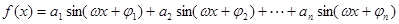 时,(其中
时,(其中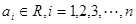 ,
,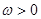 ),若
),若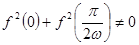 ,且函数
,且函数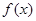 的图像关于点
的图像关于点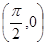 对称,在
对称,在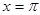 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。
(本小题满分18分)设数列{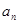 }的前
}的前 项和为
项和为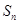 ,且满足
,且满足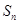 =2-
=2-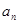 ,(
,( =1,2,3,…)
=1,2,3,…)
(Ⅰ)求数列{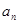 }的通项公式;
}的通项公式;
(Ⅱ)若数列{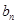 }满足
}满足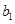 =1,且
=1,且 ,求数列{
,求数列{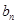 }的通项公式;
}的通项公式;
(Ⅲ)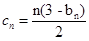 ,求
,求 的前
的前 项和
项和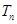
(本小题满分18分)已知函数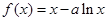 ,
,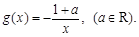
(Ⅰ)若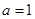 ,求函数
,求函数 的极值;
的极值;
(Ⅱ)设函数 ,求函数
,求函数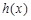 的单调区间;
的单调区间;
(Ⅲ)若在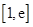 (
(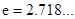 )上存在一点
)上存在一点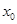 ,使得
,使得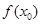
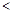
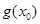 成立,求
成立,求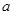 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com