
4.(2006年全国卷II)已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 ( )
(A)2 (B)6 (C)4 (D)12
3.已知两定点 、
、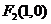 且
且 是
是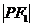 与
与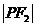 的等差中项,则动点P的轨迹方程是( )
的等差中项,则动点P的轨迹方程是( )
(A) 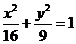 (B)
(B)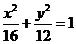 (C)
(C)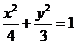 (D)
(D) 
2.已知F1,F2是椭圆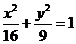 的两个焦点,过F2的直线交椭圆于A、B,若|AB|=5,则
的两个焦点,过F2的直线交椭圆于A、B,若|AB|=5,则
|A F1|+|B F1|=( )
(A)11 (B)10 (C)9 (D)16
1.椭圆5x2+ky2=5的一个焦点是(0,2),那么k等于( )
(A)-1
(B)1
(C) (D)
-
(D)
-
4.求椭圆标准方程的常用方法是待定系数法和轨迹方程法。直线与椭圆相交时的弦的中点坐标或弦中点的轨迹方程则由韦达定理来解决,设点而不求点是解析几何中的重要方法之一。另外,利用直线、弦长、圆锥曲线三者间的关系组成各类试题是解析几何中长盛不衰的主题,其中利用直线方程、直线与椭圆相交后的弦求椭圆方程是各类试题中最难的试题,也是高考的热点题型之一。
[基础闯关]
3.涉及到直线与椭圆的位置关系问题时,可以通过讨论椭圆方程与直线方程组的实数解的个数来确定,通常来说消元后得到一个关于x或y的一元二次方程,要注意判别式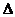 及韦达定理的运用,特别是方程思想、整体思想在解题过程中的应用。
及韦达定理的运用,特别是方程思想、整体思想在解题过程中的应用。
2.通过对椭圆的范围、对称性、特殊点(顶点、焦点、中心)、准线、对称轴及其它特性的讨论从整体上把握椭圆的形状、大小和位置,进而掌握椭圆的性质。因此在复习中就注意图形与性质对照,方程与性质对照来理解,只有通过数形结合的方式才能牢固掌握椭圆的几何性质。由椭圆的定义得到椭圆上任意一点到焦点的距离(即焦半径)公式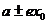 (或
(或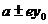 )在解题中有着重要的作用。
)在解题中有着重要的作用。
|
|
焦点在x轴上 |
焦点在y轴上 |
|
标准方程 |
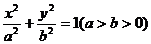 |
 |
|
图 形 |
 |
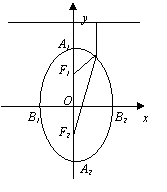 |
|
焦点坐标 |
F1( ),F2(c,0) |
F1(0,c),F2( ) |
|
对称性 |
关于x,y轴成中心对称 关于原点成中心对称 |
|
|
顶点坐标 |
A1(-a,0),A2( ) B1( ),B2(0,b) |
A1( ),A2(0,a) B1(-b,0),B2( ) |
|
范围 |
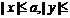 |
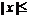 , ,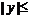 |
|
长轴短轴 |
长轴A1A2的长为 短轴B1B2的长为 |
长轴A1A2的长为 短轴B1B2的长为 |
|
离心率 |
椭圆的焦距与长轴长的比e= |
椭圆的焦距与长轴长的比e= |
|
准线方程 |
x=
|
y=
|
[特别提醒]
1.本部分的重点是掌握椭圆的定义,离心率与a,b,c之间的关系和椭圆方程的求法,定义和性质的应用是椭圆知识的重点。突破重点的关键,一是要掌握好定义的几何条件,即椭圆=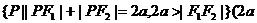 是常数
是常数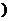 ;二是要熟练掌握椭圆标准方程的求法及其特点,运用定义时要注意隐含条件
;二是要熟练掌握椭圆标准方程的求法及其特点,运用定义时要注意隐含条件 ,明确离心率
,明确离心率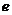 确定椭圆的形状。
确定椭圆的形状。
3.当椭圆的焦点在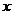 轴上时,椭圆的标准方程为
轴上时,椭圆的标准方程为  ,其中焦点坐标为
,其中焦点坐标为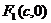 ,
,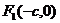 ,且
,且 ;
;
当椭圆的焦点在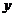 轴上时,椭圆的标准方程为
轴上时,椭圆的标准方程为  ,其中焦点坐标为
,其中焦点坐标为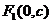 ,
,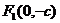 ,且
,且 .
.
当且仅当椭圆的中心在坐标原点,其焦点在坐标轴上时,椭圆的方程才是标准形式。
2.椭圆的第二定义:平面内,到定点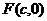 的距离与到定直线
的距离与到定直线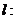 的距离之比是常数
的距离之比是常数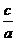 (即 )的动点的轨迹叫做椭圆,其中常数
(即 )的动点的轨迹叫做椭圆,其中常数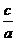 叫做椭圆的 。
叫做椭圆的 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com