
20.解:(1)PB//平面EAC。 2分
(2)
正三角形PAD中,E为PD的中点,所以, ,
,
又 ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
 (3)在PC上取点M使得
(3)在PC上取点M使得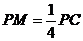 。
。
由于正三角形PAD及矩形ABCD,且AD=AB,所以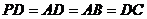
所以,在等腰直角三角形DPC中,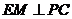 ,
,
连接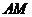 ,因为AE⊥平面PCD,所以,
,因为AE⊥平面PCD,所以,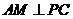 。
。
所以,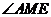 为二面角A-PC-D的平面角。
为二面角A-PC-D的平面角。
在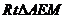 中,
中,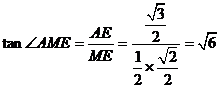 。
。
即二面角A-PC-D的正切值为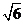 。 10分
。 10分
(4)设N为AD中点,连接PN,则 。
。
又面PAD⊥底面ABCD,所以,PN⊥底面ABCD。
所以,NB为PB在面ABCD上的射影。
 要使PB⊥AC,需且只需NB⊥AC
要使PB⊥AC,需且只需NB⊥AC
在矩形ABCD中,设AD=1,AB=x
则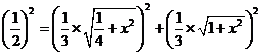 ,
,
解之得: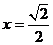 。
。
所以,当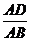
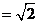 时,PB⊥AC。 14分
时,PB⊥AC。 14分
证法二:(按解法一相应步骤给分)
设N为AD中点,Q为BC中点,则因为 PAD是正三角形,底面ABCD是矩形,所以,
PAD是正三角形,底面ABCD是矩形,所以, ,
,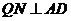 ,又因为侧面PAD⊥底面ABCD,所以,
,又因为侧面PAD⊥底面ABCD,所以,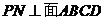 ,
,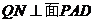 ,
,
以N为坐标原点,NA、NQ、NP所在直线分别为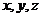 轴如图建立空间直角坐标系。设
轴如图建立空间直角坐标系。设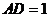 ,
, ,则
,则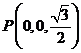 ,
,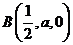 ,
,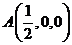 ,
,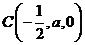 ,
,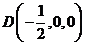 ,
,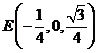 。
。
(2)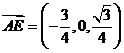 ,
, ,
,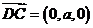 ,
,
 ,
,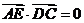
所以,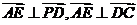 。
。
又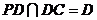 ,
,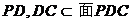 ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
(3)当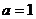 时,由(2)可知:
时,由(2)可知: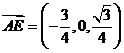 是平面PDC的法向量;
是平面PDC的法向量;
设平面PAC的法向量为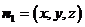 ,则
,则 ,
,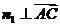 ,即
,即
 ,取
,取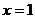 ,可得:
,可得: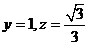 。所以,
。所以, 。
。
向量 与
与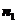 所成角
所成角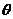 的余弦值为:
的余弦值为: 。
。
所以,tan q = 。
又由图可知,二面角A-PC-D的平面角为锐角,所以,二面角A-PC-D的平面角就是向量 与
与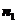 所成角
所成角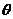 的补角。
的补角。
其正切值等于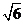 。 10分
。 10分
(4) ,
,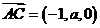 ,令
,令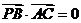 ,得
,得 ,所以,
,所以,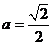 。所以,当
。所以,当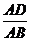
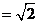 时,PB⊥AC。
时,PB⊥AC。
19.解:⑴由已知f′(x)=-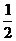 e-x(ax2+a+1)+
e-x(ax2+a+1)+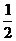 e-x·2ax
e-x·2ax
=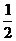 e-x(-ax2+2ax-a-1)
e-x(-ax2+2ax-a-1)
∴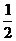 e-x>0,以下讨论函数g(x)=-ax2+2ax-a-1
e-x>0,以下讨论函数g(x)=-ax2+2ax-a-1
当a=0时,g(x)=-1<0,即f′(x)<0,∴f(x)是R上是减函数
当a>0时,g(x)=0的判断式:△=4a2-4(a2+a)=-4a<0
∴g(x)<0即f′(x)<0, ∴f(x)在R上是减函数。
当a<0时,g(x)=0有两个根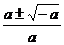 ,且
,且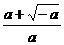 <
<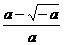
∴在(-∞,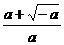 )上,g(x)>0,即f′(x)>0,f(x)在此区间上是增函数。
)上,g(x)>0,即f′(x)>0,f(x)在此区间上是增函数。
在(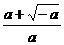 ,
,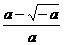 )上,g(x)<0,即f′(x)<0
)上,g(x)<0,即f′(x)<0
f(x)在区间上是减函数,在(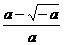 ,+∞)上,g(x)>0,即f′(x)>0
,+∞)上,g(x)>0,即f′(x)>0
f(x)在此区间上是增函数。
⑵当-1<a<0时,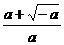 =1+
=1+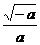 <1,
<1,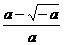 =1+
=1+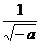 >2,∴在区间[1,2]上,函数f(x)单调递减
>2,∴在区间[1,2]上,函数f(x)单调递减
∴函数f(x)在[1,2]上的最小值为f(2)=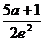
18.解:(1)
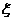 |
3 |
4 |
5 |
6 |
|
P |
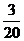 |
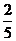 |
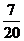 |
 |
(2)
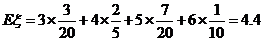
17.解:(1)∵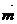 =(sinB,1-cosB)
, 且与向量
=(sinB,1-cosB)
, 且与向量 (2,0)所成角为
(2,0)所成角为
∴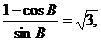 ∴tan
∴tan
(2)由(1)可得
 ’
’
∵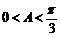 ∴
∴ ∴
∴ .
.
当且仅当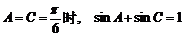
13. 11;1  4.
4. 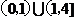 ;15.
;15. ; 16.①③
; 16.①③
22.(本题满分14分)已知方向向量为 的直线l过点A(
的直线l过点A(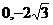 )和椭圆
)和椭圆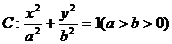 的焦点,
的焦点,
且椭圆C的中心O和椭圆的右准线上的点B满足: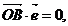 . |
. | |
|
(1)求椭圆C的方程;
(2)设M、N是椭圆C上两个不同点,且M、N的纵坐标之和为1,记u为M、N的横坐标之积.问是否存在最小的常数m ,
使u≤m恒成立?若存在,求出m的值;若不存在,说明理由.
|
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟
第Ⅰ卷(选择题,共60分)
21.(本题满分12分)设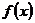 =
=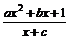 (a>0)为奇函数,且
(a>0)为奇函数,且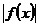 min=
min=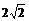 ,
,
数列{an}与{bn}满足如下关系:a1=2, 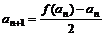 ,
,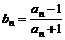 .
.
(1)求f(x)的解析表达式;
(2) 证明:当n∈N+时, 有bn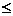
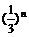 .
.
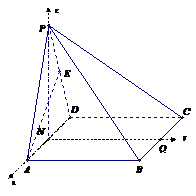
20. (本题满分12分)如图,四棱锥P -ABCD的底面是矩形,侧面PAD是
正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(本题满分12分)如图,四棱锥P -ABCD的底面是矩形,侧面PAD是
正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)试判断直线PB与平面EAC的关系(不必证明);
(2)求证:AE⊥平面PCD;
(3)若AD = AB,试求二面角A-PC-D的正切值;
(4)当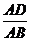 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
19.(本题满分12分)设a∈R,函数f(x)=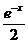 (ax2+a+1),其中e是自然对数的底数。
(ax2+a+1),其中e是自然对数的底数。
⑴判断f(x)在R上的单调性;
⑵当-1<a<0时,求f(x)在[1,2]上的最小值。
18.(本题满分12分).有甲、乙、丙、丁四支球队进行单循环比赛,最后据各队积分决出名次.规定每场比赛必须决出胜负,其中胜方积2分,负方积1分,已知球队甲与球队乙对阵,甲队取胜的概率为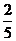 ,与球队丙、丁对阵,甲队取胜的概率均为
,与球队丙、丁对阵,甲队取胜的概率均为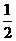 ,且各场次胜负情况彼此没有影响.
,且各场次胜负情况彼此没有影响.
(1)甲队至少胜一场的概率; (2)求球队甲赛后积分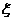 的概率分布和数学期望.
的概率分布和数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com