
23.(本题满分12分)
已知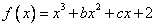
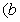 、
、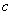 为实数)、
为实数)、
(I)若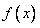 在
在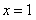 时,有极值-1,求
时,有极值-1,求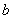 、
、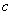 的值;
的值;
(II)若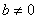 ,证明函数
,证明函数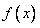 的图像图存在与直线
的图像图存在与直线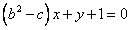 平行的切线。
平行的切线。
22.(本题满分10分)
对于命题“若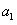 、
、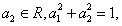 则
则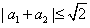 ”,有如下证明:
”,有如下证明:
构造函数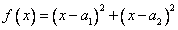 ,则
,则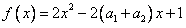 ,因为对一切
,因为对一切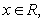 恒有
恒有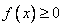 ,所以
,所以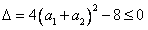 ,故
,故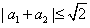 。
。
试解决下列问题:
(I)若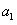 、
、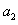 、
、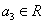 ,
,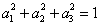 ,求证:
,求证: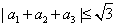 ;、
;、
(II)试将上述敏体推广到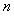 个实数的情况。(只需写出命题,不要求证明)
个实数的情况。(只需写出命题,不要求证明)
21.已知命题: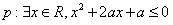 是假命题,则实数
是假命题,则实数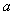 的取值范围是
。
的取值范围是
。
20.用火柴棒“金鱼”图,如图所示:

按照上面的规律,第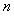 个“金鱼”图需要火柴棒的根数为
。
个“金鱼”图需要火柴棒的根数为
。
19.某工程由 、
、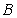 、
、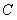 、
、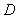 四道工序组成,完成它们需用的时间依次是2,5,
四道工序组成,完成它们需用的时间依次是2,5,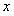 ,4天。四道工序的先后顺序及相互关系是:
,4天。四道工序的先后顺序及相互关系是: 、
、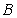 工序可以同时开工;A完成后,C可以开工;B、C工序完成后,D可以开工。若完成该工程总时数为9天,则完成工序C需用的天数
工序可以同时开工;A完成后,C可以开工;B、C工序完成后,D可以开工。若完成该工程总时数为9天,则完成工序C需用的天数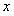 最大是
。
最大是
。
18.某抛物线型拱桥,拱桥的顶点距水面2米,桥拱水面宽度为8米,暴雨过后,河面上升,当水面上升1米,桥拱水面宽度为 米。
17.(本题满分12分)
设函数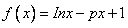 ,其中
,其中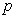 为实数,且
为实数,且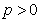 ,若对任意的
,若对任意的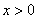 ,恒有
,恒有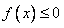 ,求
,求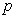 的取值范围。
的取值范围。
B卷(共50分)
16.(本题满分12分)
为了研究某种产品的销售额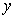 (万元)随广告费用支出
(万元)随广告费用支出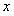 (万元)的变化情况,收集数据如下:
(万元)的变化情况,收集数据如下:
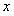 |
2 |
4 |
5 |
6 |
8 |
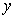 |
30 |
40 |
60 |
50 |
70 |
用广告费用支出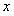 (万元)作为解释变量,产品的销售额
(万元)作为解释变量,产品的销售额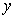 (万元)作为预报变量。
(万元)作为预报变量。
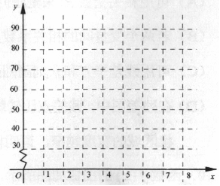
(I)作出数据的散点图;
(II)描述解释变量与预报变量之间的关系,并求出回归
方程;
(III)据此估计当广告费用支出10万元时产品的销售额收入。
15.(本题满分10分)
点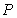 在抛物线
在抛物线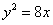 上,若
上,若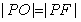 ,其中
,其中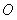 为坐标原点,
为坐标原点,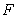 是抛物线的焦点,试求点
是抛物线的焦点,试求点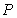 的坐标。
的坐标。
14.已知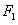 、
、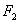 是椭圆
是椭圆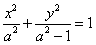 的左、右焦点,弦
的左、右焦点,弦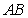 过点
过点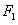 ,若
,若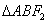 的周长为12,则椭圆的方程为
。
的周长为12,则椭圆的方程为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com