
5.在等差数列{a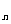 }中,已知a
}中,已知a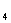 + a
+ a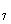 + a
+ a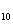 = 17,a
= 17,a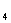 + a
+ a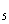 + a
+ a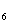 + ┄ + a
+ ┄ + a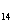 = 77, 若a
= 77, 若a =13,则k等于
=13,则k等于
A. 16 B. 18 C. 20 D. 22
4、等比数列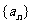 中,已知
中,已知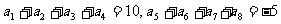 ,则数列
,则数列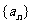 的前16项和S16为
的前16项和S16为
A.-50 B.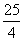 C.
C.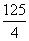 D.
D.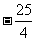
3、 等差数列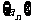 中,
中,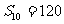 ,那么
,那么 的值是
的值是
(A) 12 (B) 24 (C) 16 (D) 48
2. 若数列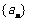 的前n项和为Sn=3n+a,若数列
的前n项和为Sn=3n+a,若数列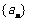 为等比数列,则实数a的取值是
为等比数列,则实数a的取值是
A、3 B、 1 C、 0 D、-1
1. 在公比为整数的等比数列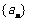 中,如果
中,如果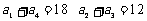 ,则这个等比数列前8项的和为
,则这个等比数列前8项的和为
A.513
B.512
C.510
D.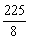
203.实系数一元二次方程的解
实系数一元二次方程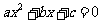 ,
,
①若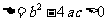 ,则
,则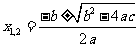 ;
;
②若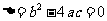 ,则
,则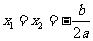 ;
;
③若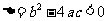 ,它在实数集
,它在实数集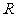 内没有实数根;在复数集
内没有实数根;在复数集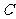 内有且仅有两个共轭复数根
内有且仅有两个共轭复数根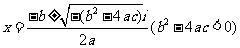 .
.
148.柱体、锥体的体积
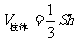 (
(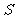 是柱体的底面积、
是柱体的底面积、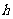 是柱体的高).
是柱体的高).
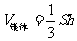 (
(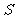 是锥体的底面积、
是锥体的底面积、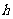 是锥体的高).
是锥体的高).
排列组合
l 分类计数原理(加法原理)
 .
.
l 分步计数原理(乘法原理)
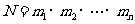 .
.
l 排列数公式
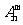 =
=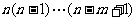 =
=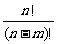 .(
.(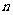 ,
,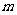 ∈N*,且
∈N*,且 ).
).
注:规定 .
.
l 排列恒等式
(1) ;
;
(2)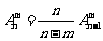 ;
;
(3)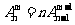 ;
;
(4)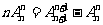 ;
;
(5)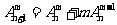 .
.
(6) 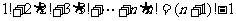 .
.
l 组合数公式
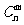 =
=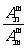 =
=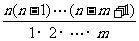 =
=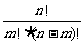 (
(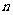 ∈N*,
∈N*, ,且
,且 ).
).
l 组合数的两个性质
(1)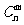 =
=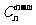 ;
;
(2) 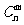 +
+ =
=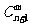 .
.
注:规定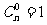 .
.
l 组合恒等式
(1)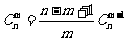 ;
;
(2)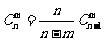 ;
;
(3)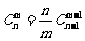 ;
;
(4)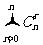 =
=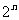 ;
;
(5)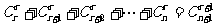 .
.
(6)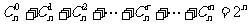 .
.
(7)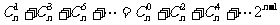 .
.
(8)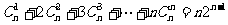 .
.
(9) .
.
(10)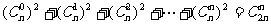 .
.
l 排列数与组合数的关系
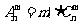 .
.
l 单条件排列
以下各条的大前提是从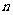 个元素中取
个元素中取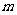 个元素的排列.
个元素的排列.
(1)“在位”与“不在位”
①某(特)元必在某位有 种;②某(特)元不在某位有
种;②某(特)元不在某位有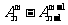 (补集思想)
(补集思想)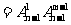 (着眼位置)
(着眼位置)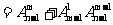 (着眼元素)种.
(着眼元素)种.
(2)紧贴与插空(即相邻与不相邻)
①定位紧贴: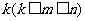 个元在固定位的排列有
个元在固定位的排列有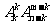 种.
种.
②浮动紧贴: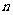 个元素的全排列把k个元排在一起的排法有
个元素的全排列把k个元排在一起的排法有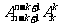 种.注:此类问题常用捆绑法;
种.注:此类问题常用捆绑法;
③插空:两组元素分别有k、h个(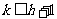 ),把它们合在一起来作全排列,k个的一组互不能挨近的所有排列数有
),把它们合在一起来作全排列,k个的一组互不能挨近的所有排列数有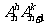 种.
种.
(3)两组元素各相同的插空
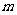 个大球
个大球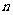 个小球排成一列,小球必分开,问有多少种排法?
个小球排成一列,小球必分开,问有多少种排法?
当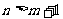 时,无解;当
时,无解;当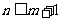 时,有
时,有 种排法.
种排法.
(4)两组相同元素的排列:两组元素有m个和n个,各组元素分别相同的排列数为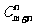 .
.
l 分配问题
(1)(平均分组有归属问题)将相异的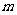 、
、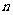 个物件等分给
个物件等分给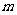 个人,各得
个人,各得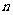 件,其分配方法数共有
件,其分配方法数共有 .
.
(2)(平均分组无归属问题)将相异的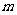 ·
·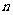 个物体等分为无记号或无顺序的
个物体等分为无记号或无顺序的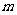 堆,其分配方法数共有
堆,其分配方法数共有
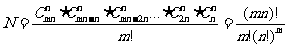 .
.
(3)(非平均分组有归属问题)将相异的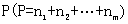 个物体分给
个物体分给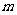 个人,物件必须被分完,分别得到
个人,物件必须被分完,分别得到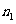 ,
,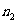 ,…,
,…,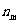 件,且
件,且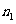 ,
,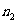 ,…,
,…,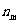 这
这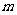 个数彼此不相等,则其分配方法数共有
个数彼此不相等,则其分配方法数共有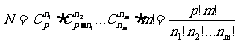 .
.
(4)(非完全平均分组有归属问题)将相异的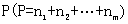 个物体分给
个物体分给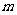 个人,物件必须被分完,分别得到
个人,物件必须被分完,分别得到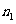 ,
,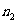 ,…,
,…,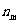 件,且
件,且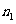 ,
,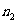 ,…,
,…,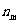 这
这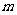 个数中分别有a、b、c、…个相等,则其分配方法数有
个数中分别有a、b、c、…个相等,则其分配方法数有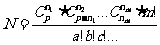
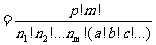 .
.
(5)(非平均分组无归属问题)将相异的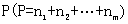 个物体分为任意的
个物体分为任意的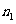 ,
,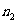 ,…,
,…,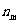 件无记号的
件无记号的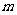 堆,且
堆,且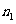 ,
,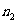 ,…,
,…,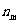 这
这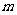 个数彼此不相等,则其分配方法数有
个数彼此不相等,则其分配方法数有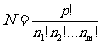 .
.
(6)(非完全平均分组无归属问题)将相异的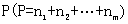 个物体分为任意的
个物体分为任意的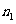 ,
,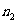 ,…,
,…,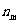 件无记号的
件无记号的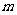 堆,且
堆,且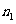 ,
,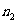 ,…,
,…,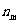 这
这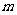 个数中分别有a、b、c、…个相等,则其分配方法数有
个数中分别有a、b、c、…个相等,则其分配方法数有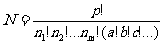 .
.
(7)(限定分组有归属问题)将相异的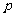 (
(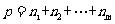 )个物体分给甲、乙、丙,……等
)个物体分给甲、乙、丙,……等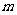 个人,物体必须被分完,如果指定甲得
个人,物体必须被分完,如果指定甲得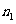 件,乙得
件,乙得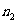 件,丙得
件,丙得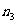 件,…时,则无论
件,…时,则无论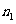 ,
,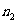 ,…,
,…,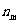 等
等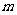 个数是否全相异或不全相异其分配方法数恒有
个数是否全相异或不全相异其分配方法数恒有
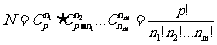 .
.
l “错位问题”及其推广
贝努利装错笺问题:信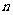 封信与
封信与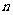 个信封全部错位的组合数为
个信封全部错位的组合数为
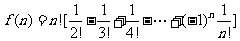 .
.
推广: 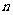 个元素与
个元素与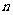 个位置,其中至少有
个位置,其中至少有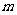 个元素错位的不同组合总数为
个元素错位的不同组合总数为

 .
.
l
不定方程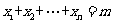 的解的个数
的解的个数
(1)方程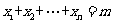 (
(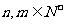 )的正整数解有
)的正整数解有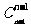 个.
个.
(2) 方程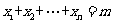 (
(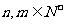 )的非负整数解有
)的非负整数解有 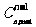 个.
个.
(3) 方程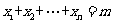 (
(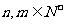 )满足条件
)满足条件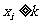 (
(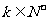 ,
,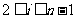 )的非负整数解有
)的非负整数解有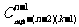 个.
个.
(4) 方程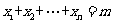 (
(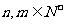 )满足条件
)满足条件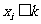 (
(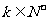 ,
,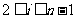 )的正整数解有
)的正整数解有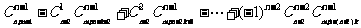 个.
个.
l
二项式定理 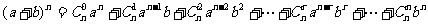 ;
;
二项展开式的通项公式
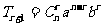
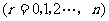 .
.
概率
l 等可能性事件的概率
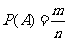 .
.
l 互斥事件A,B分别发生的概率的和
P(A+B)=P(A)+P(B).
l
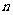 个互斥事件分别发生的概率的和
个互斥事件分别发生的概率的和
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
l 独立事件A,B同时发生的概率
P(A·B)= P(A)·P(B).
l .n个独立事件同时发生的概率
P(A1· A2·…· An)=P(A1)· P(A2)·…· P(An).
l n次独立重复试验中某事件恰好发生k次的概率
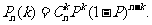 \
\
期望与方差
l .离散型随机变量的分布列的两个性质
(1)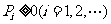 ;
;
(2)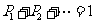 .
.
l 数学期望
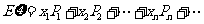
l 数学期望的性质
(1) .
.
(2)若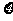 -
-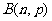 ,则
,则 .
.
(3) 若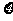 服从几何分布,且
服从几何分布,且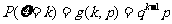 ,则
,则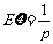 .
.
l 方差
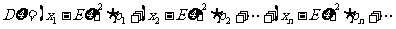
l 标准差
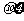 =
=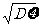 .
.
l 方差的性质
(1)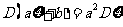 ;
;
(2)若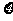 -
-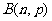 ,则
,则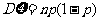 .
.
(3) 若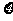 服从几何分布,且
服从几何分布,且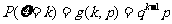 ,则
,则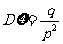 .
.
l 方差与期望的关系
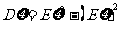 .
.
l 正态分布密度函数
 ,式中的实数μ,
,式中的实数μ,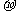 (
(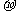 >0)是参数,分别表示个体的平均数与标准差.
>0)是参数,分别表示个体的平均数与标准差.
l .标准正态分布密度函数
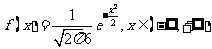 .
.
l
.对于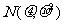 ,取值小于x的概率
,取值小于x的概率
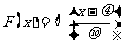 .
.
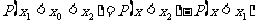
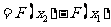
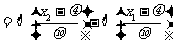 .
.
l 回归直线方程
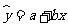 ,其中
,其中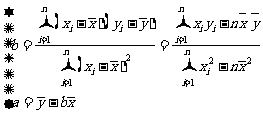 .
.
l 相关系数
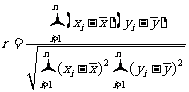
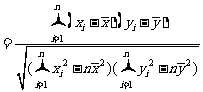 .
.
|r|≤1,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小.
极限
l .特殊数列的极限
(1) .
.
(2)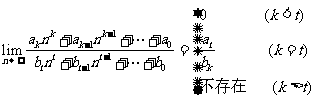 .
.
(3)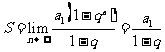 (
(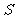 无穷等比数列
无穷等比数列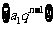 (
(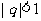 )的和).
)的和).
l 函数的极限定理
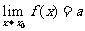
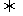
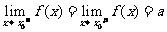 .
.
l .函数的夹逼性定理
如果函数f(x),g(x),h(x)在点x0的附近满足:
(1)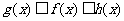 ;
;
(2)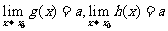 (常数),
(常数),
则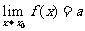 .
.
本定理对于单侧极限和 的情况仍然成立.
的情况仍然成立.
l 几个常用极限
(1)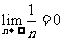 ,
,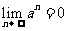 (
(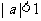 );
);
(2)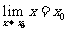 ,
, .
.
l 两个重要的极限
(1)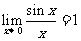 ;
;
(2)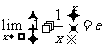 (e=2.718281845…).
(e=2.718281845…).
l .函数极限的四则运算法则
若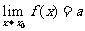 ,
,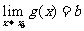 ,则
,则
(1)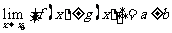 ;
;
(2)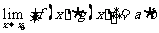 ;
;
(3)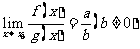 .
.
l .数列极限的四则运算法则
若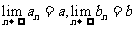 ,则
,则
(1)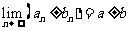 ;
;
(2)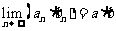 ;
;
(3)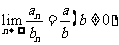
(4) ( c是常数).
( c是常数).
导数
l
.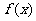 在
在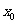 处的导数(或变化率或微商)
处的导数(或变化率或微商)
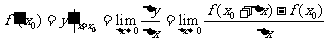 .
.
l 瞬时速度
 .
.
l 瞬时加速度
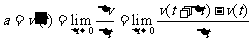 .
.
l
.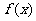 在
在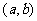 的导数
的导数
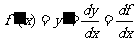
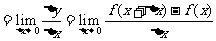 .
.
l
. 函数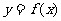 在点
在点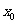 处的导数的几何意义
处的导数的几何意义
函数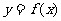 在点
在点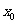 处的导数是曲线
处的导数是曲线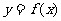 在
在 处的切线的斜率
处的切线的斜率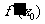 ,相应的切线方程是
,相应的切线方程是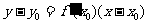 .
.
l .几种常见函数的导数
(1)
 (C为常数).
(C为常数).
(2)
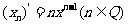 .
.
(3)
 .
.
(4)
 .
.
(5) 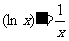 ;
;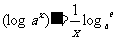 .
.
(6)
 ;
;
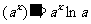 .
.
l .导数的运算法则
(1)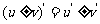 .
.
(2)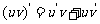 .
.
(3)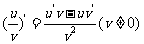 .
.
l .复合函数的求导法则
设函数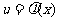 在点
在点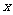 处有导数
处有导数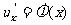 ,函数
,函数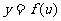 在点
在点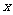 处的对应点U处有导数
处的对应点U处有导数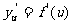 ,则复合函数
,则复合函数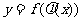 在点
在点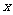 处有导数,且
处有导数,且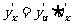 ,或写作
,或写作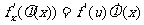 .
.
l
常用的近似计算公式(当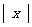 充小时)
充小时)
(1)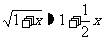 ;
; ;
;
(2)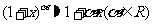 ;
; 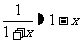 ;
;
(3)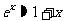 ;
;
(4)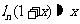 ;
;
(5)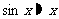 (
(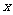 为弧度);
为弧度);
(6)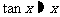 (
(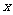 为弧度);
为弧度);
(7)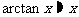 (
(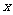 为弧度)
为弧度)
l
.判别 是极大(小)值的方法
是极大(小)值的方法
当函数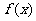 在点
在点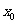 处连续时,
处连续时,
(1)如果在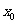 附近的左侧
附近的左侧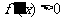 ,右侧
,右侧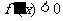 ,则
,则 是极大值;
是极大值;
(2)如果在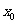 附近的左侧
附近的左侧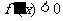 ,右侧
,右侧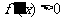 ,则
,则 是极小值.
是极小值.
.复数的相等
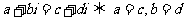 .(
.(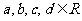 )
)
l
.复数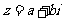 的模(或绝对值)
的模(或绝对值)
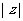 =
= =
=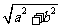 .
.
l .复数的四则运算法则
(1) ;
;
(2)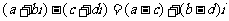 ;
;
(3)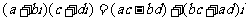 ;
;
(4) .
.
l .复数的乘法的运算律
对于任何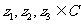 ,有
,有
交换律: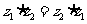 .
.
结合律: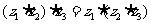 .
.
分配律: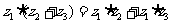 .
.
l .复平面上的两点间的距离公式
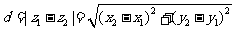 (
(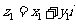 ,
,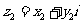 ).
).
l .向量的垂直
非零复数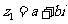 ,
,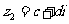 对应的向量分别是
对应的向量分别是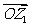 ,
,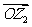 ,则
,则
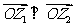
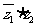 的实部为零
的实部为零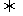
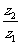 为纯虚数
为纯虚数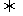
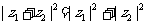
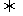
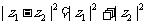
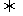
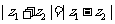
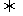
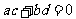
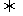
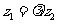 (λ为非零实数).
(λ为非零实数).
147.球的组合体
(1)球与长方体的组合体:
长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:
正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.
(3) 球与正四面体的组合体:
棱长为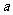 的正四面体的内切球的半径为
的正四面体的内切球的半径为 ,外接球的半径为
,外接球的半径为 .
.
146.球的半径是R,则
其体积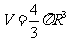 ,
,
其表面积 .
.
145.欧拉定理(欧拉公式)
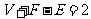 (简单多面体的顶点数V、棱数E和面数F).
(简单多面体的顶点数V、棱数E和面数F).
(1)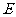 =各面多边形边数和的一半.特别地,若每个面的边数为
=各面多边形边数和的一半.特别地,若每个面的边数为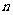 的多边形,则面数F与棱数E的关系:
的多边形,则面数F与棱数E的关系: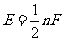 ;
;
(2)若每个顶点引出的棱数为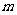 ,则顶点数V与棱数E的关系:
,则顶点数V与棱数E的关系: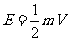 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com