
6.食品安全已成为近几年来社会关注的人点问题之一。下列有关食品添加剂使用的说法正确的是
A.为了调节食品色泽,改善食品外观,使用工业色素苏丹红
B.为了提高奶粉中氮含量,加入适量的三聚氰胺
C.为了防止食品腐败,加入适量苯甲酸钠以达到抑制细菌繁殖的作用
D.为了补充食物中缺乏的微量元素碘,在食盐中加入少量的碘单质
5.下图是用集合的方法,表示各种概念之间的关系,其中与图示相符的是
|
选项 |
1 |
2 |
3 |
4 |
|
A |
特异性免疫 |
细胞免疫 |
T细胞 |
抗体 |
|
B |
DNA |
基因 |
编码区 |
外显子 |
|
C |
无性生殖 |
营养生殖 |
嫁接 |
组织培养 |
|
D |
氮循环 |
共生 |
固氮菌 |
生物固氮 |
4.以下说法正确的是 A.抗体的分泌属于体液免疫的反应阶段
B.紫茉莉的遗传物质的载体是染色体、线粒体和叶绿体 C.C3植物维管束鞘细胞与高等动物细胞在结构上的区别主要是前者有叶绿体、液泡和
细胞壁,而后者有中心体 D.质粒、PEG、生长激素三种物质的化学本质依次是DNA、聚乙二醇和吲哚乙酸
3.组织液大量积累在组织间隙会导致组织水肿。下列各项不引起组织水肿的是
A.营养不良,血浆蛋白含量减少 B.花粉过敏引起毛细血管通透性增加
C.肾小球肾炎导致蛋白尿 D.食物过咸导致血浆渗透压增高
2. 一种新发现的细菌质粒中有a、b、c等基因,右图表示用限制性内切酶处理后得到的片段。下列有关叙述中不正确的是
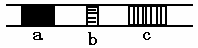 A.基因a、b、c在生命活动过程中选择性表达
A.基因a、b、c在生命活动过程中选择性表达
B.基因a控制合成的蛋白质含有m个氨基酸,比水稻中控制
合成含有m个氨基酸的蛋白质的基因长度要短很多
C.若利用某药物阻止基因a的表达,则基因b、c也不能表达
D.组成基因a、b、c的基本单位相同,而且基因a、b、c中都有RNA聚合酶的结合位点
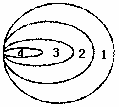
1.下图显示四种细菌(1、2、3、4)对琼脂板 上的抗生素X的不同反应,请问哪种细菌对 抗生素X的抗药性最强
抗生素X的抗药性最强
A.细菌1
B.细菌2
C.细菌3
D.细菌4
22、解:(Ⅰ)当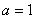 时,
时,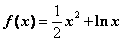 ,
,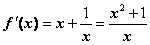 ;………2分
;………2分
对于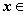 [1,e],有
[1,e],有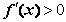 ,∴
,∴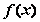 在区间[1,e]上为增函数,…3分
在区间[1,e]上为增函数,…3分
∴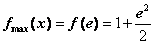 ,
,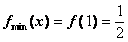 .……………………………5分
.……………………………5分
(Ⅱ)令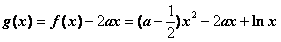 ,
,
则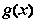 的定义域为(0,+∞).…………6分
的定义域为(0,+∞).…………6分
在区间(1,+∞)上函数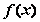 的图象恒在直线
的图象恒在直线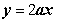 下方等价于
下方等价于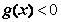 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵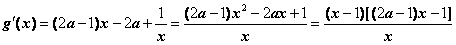
① 若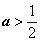 ,令
,令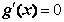 ,得极值点
,得极值点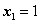 ,
,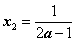 ,
,
当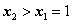 ,即
,即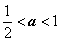 时,在(
时,在(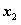 ,+∞)上有
,+∞)上有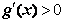 ,
,
此时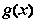 在区间(
在区间(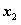 ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有
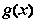 ∈(
∈(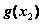 ,+∞),不合题意;………………………………………8分
,+∞),不合题意;………………………………………8分
当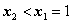 ,即
,即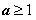 时,同理可知,
时,同理可知,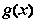 在区间(1,+∞)上,有
在区间(1,+∞)上,有
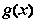 ∈(
∈(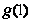 ,+∞),也不合题意;………………………………………9分
,+∞),也不合题意;………………………………………9分
② 若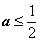 ,则有
,则有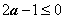 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有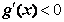 ,
,
从而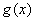 在区间(1,+∞)上是减函数;……………………………………10分
在区间(1,+∞)上是减函数;……………………………………10分
要使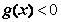 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足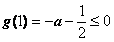
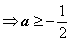 ,
,
由此求得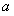 的范围是[
的范围是[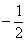 ,
,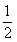 ].
].
综合①②可知,当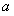 ∈[
∈[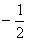 ,
,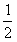 ]时,
]时,
函数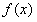 的图象恒在直线
的图象恒在直线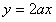 下方. ………………12分
下方. ………………12分
21、解:(Ⅰ)已知式即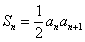 ,故
,故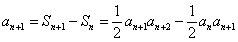 .
.
因为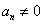 ,当然
,当然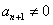 ,所以
,所以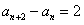
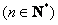 .
.
由于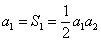 ,且
,且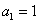 ,故
,故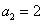 .
.
于是 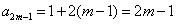 ,
,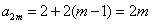 ,
,
所以 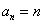
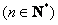 .
……………4分
.
……………4分
(Ⅱ)由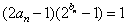 ,得
,得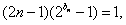
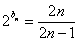 ,
,
故 .从而
.从而 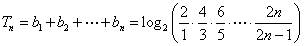 .
.
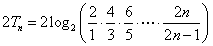
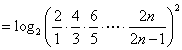
因此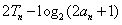
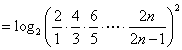
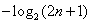
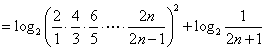
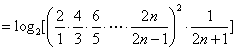 .
.
设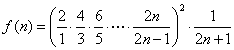 ,
,
则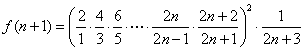 ,
,
故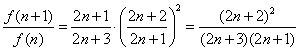
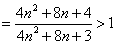 ,
,
注意到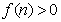 ,所以
,所以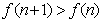 .
.
特别地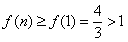 ,从而
,从而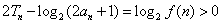 .
.
所以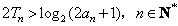 .
………………12分
.
………………12分
22.(本小题满分12分)已知函数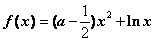 .(
.(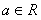 )
)
(Ⅰ)当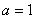 时,求
时,求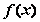 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数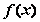 的图象恒在直线
的图象恒在直线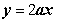 下方,求
下方,求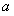 的取值范围.
的取值范围.

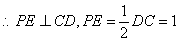 又平面
又平面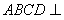 平面
平面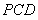
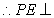 平面
平面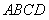 。
。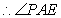 就是
就是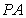 与平面
与平面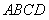 所成的角。……6分
所成的角。……6分
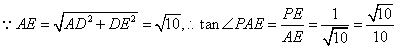 ………………………7分
………………………7分
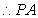 与平面
与平面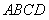 所成的角的正切值为
所成的角的正切值为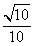 ………8分
………8分
(3)解:当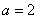 时,
时,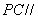 平面
平面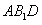 ………9分由
………9分由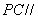 平面
平面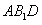 ,
,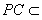 平面
平面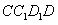 ,平面
,平面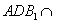 平面
平面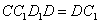
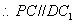 ,又
,又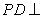 平面
平面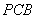 ,
,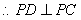 ,因而
,因而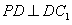 …10分又
…10分又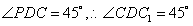 即
即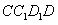 是正方形,
是正方形,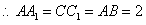 …………………12分
…………………12分
21、(本小题满分12分)
已知数列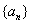 的前
的前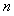 项和为
项和为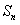 ,且
,且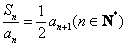 ,其中
,其中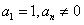 .
.
(Ⅰ)求数列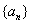 的通项公式;
的通项公式;
(Ⅱ)设数列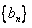 满足
满足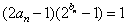 ,
,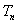 为
为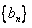 的前
的前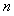 项和,求证:
项和,求证:
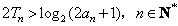 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com