
5.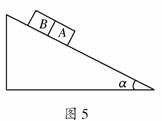 (2008·全国卷Ⅱ)如图5所示,一固定斜面上两个质量相同的小物块A和B紧挨着匀速下滑,A与B的接触面光滑.已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为α,B与斜面之间的动摩擦因数是
(2008·全国卷Ⅱ)如图5所示,一固定斜面上两个质量相同的小物块A和B紧挨着匀速下滑,A与B的接触面光滑.已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为α,B与斜面之间的动摩擦因数是
( )
A.tanα B.cotα C.tanα D.cotα
解析:A、B两物体受到斜面的支持力均为mgcosα,所受滑动摩擦力分别为:FfA=μAmgcosα,FfB=μBmgcosα,对整体受力分析结合平衡条件可得:2mgsinα=μAmgcosα+μBmgcosα,且μA=2μB,解之得μB=tanα,A项正确.
答案:A
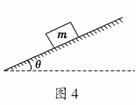
4. (2009·北京高考)如图4所示,将质量为m的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则 ( )
A.将滑块由静止释放,如果μ>tanθ,滑块将下滑
B.给滑块沿斜面向下的初速度,如果μ<tanθ,滑块将减速下滑
C.用平行于斜面向上的力拉滑块向上匀速滑动,如果μ=tanθ,拉力大小应是2mgsinθ
D.用平行于斜面向下的力拉滑块向下匀速滑动,如果μ=tanθ,拉力大小应是mgsinθ
解析:对放在斜面上的滑块进行受力分析,当mgsinθ=μmgcosθ,即μ=tanθ时,滑块受力平衡,若先前静止,则滑块静止;若有向下的初速度,则做匀速运动.A中,μ>tanθ,滑块静止在斜面上不会下滑;B中,滑块要加速下滑;C中,拉力沿斜面向上,滑动摩擦力向下,则拉力的大小为2mgsinθ;D中,滑块沿斜面向下匀速滑动,不需要外力作用.
答案:C
3.如图3所示,质量为m的木块P在质量为M的长木板ab上滑行,长木板放在水平地面上 一直处于静止状态.若长木板ab与地面间的动摩擦因数为μ1,木块P与长木板ab间的动摩擦因数为μ2,则长木板ab受到地面的摩擦力大小为
( )
一直处于静止状态.若长木板ab与地面间的动摩擦因数为μ1,木块P与长木板ab间的动摩擦因数为μ2,则长木板ab受到地面的摩擦力大小为
( )
A.μ1Mg B.μ1(m+M)g
C.μ2mg D.μ1Mg+μ2mg
解析:若长木板ab未动即地面对长木板ab的摩擦力为静摩擦力,由于P在长木板ab上滑动,即P对长木板ab的摩擦力大小为μ2mg.由平衡条件可知地面对ab的静摩擦力大小为μ2mg.即只有C正确.
 答案:C
答案:C
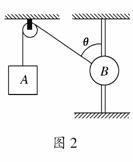
2.如图2所示,一条细绳跨过定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直杆上,两物体均保持静止,不计绳与滑轮、B与竖直杆间的摩擦,已知绳与竖直杆间的夹角θ,则物体A、B的质量之比mA∶mB等于 ( )
A.cosθ∶1 B.1∶cosθ
C.tanθ∶1 D.1∶sinθ
解析:对A、B受力分析可知mAgcosθ=mBg,则有mA∶mB=1∶cosθ,B项正确.
答案:B
1.如图1所示,质量均为m的物体A、B通过一劲度系数k的弹簧相连,开始时B放在地面上,A、B均处于静止状态,现通过细绳将A向上拉起,当B刚要离开地面时,A上升距离为L,假设弹簧一直在弹性限度内,则 ( )
A.L= B.L<
C.L= D.L>
解析:拉A之前,A静止时,mg=kx1,弹簧的压缩量为x1,当B刚要离开地面时,弹簧的伸长量为x2,mg=kx2,所以A上升的距离为L=x1+x2=,故A正确.
 答案:A
答案:A
16.(12分)质量为m=1.0 kg的小滑块(可视为质点)放在质量为M=3.0 kg的长木板的右端,
木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.2,木板长L=1.0 m.开始时两
者都处于静止状态,现对木板施加水平向右的恒力F=12 N,如图19所示,经一段时
间后撤去F.为使小滑块不掉下木板,试求:用水平恒力F作用的最长时间.(g取10 m/s2)
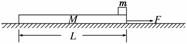
图19
解析:撤力前后木板先加速后减速,设加速过程的位移为x1,加速度为a1,加速运动的
时间为t1;减速过程的位移为x2,加速度为a2,减速运动的时间为t2.由牛顿第二定律得
撤力前:F-μ(m+M)g=Ma1
解得a1= m/s2
撤力后:μ(m+M)g=Ma2
解得a2= m/s2
x1=a1t12,x2=a2t22
为使小滑块不从木板上掉下,应满足x1+x2≤L
又a1t1=a2t2
由以上各式可解得t1≤1 s
即作用的最长时间为1 s.
答案:1 s
15.(14分)如图18(a)所示,质量m=1 kg的物体沿倾角θ=37°的固定粗糙斜面由静止开始
向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k
表示,物体加速度a与风速v的关系如图(b)所示,求:(sin37°=0.6,cos37°=0.8,g=
10 m/s2)
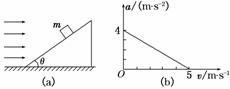
图18
(1)物体与斜面间的动摩擦因数μ;
(2)比例系数k.
解析:(1)由图象知v=0,a0=4 m/s2,得
mgsinθ-μmgcosθ=ma0
μ===0.25.
(2)由图象知v=5 m/s,a=0,得
mgsinθ-μFN-kvcosθ=0
FN=mgcosθ+kvsinθ
联立两式得
mg(sinθ-μcosθ)-kv(μsinθ+cosθ)=0
k== kg/s
=0.84 kg/s.
答案:(1)μ=0.25 (2)k=0.84 kg/s
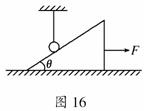 13.(10分)如图16所示,斜面体质量为M,倾角为θ,与水平面间的动
13.(10分)如图16所示,斜面体质量为M,倾角为θ,与水平面间的动
摩擦因数为μ,用细绳竖直悬挂一质量为m的小球静止在光滑斜面
上,当烧断绳的瞬间,至少以多大的水平向右的力由静止拉动斜面
体,小球才能做自由落体运动到地面?
解析:设小球自由落体运动到地面上,下落高度为h,
则斜面体至少水平向右运动的位移为:
x=h·cotθ
对小球:h=gt2
对斜面体:x=at2
由以上三式解得:a=gcotθ
以斜面体为研究对象有:F-μMg=Ma
所以F=μMg+Mgcotθ=(μ+cotθ)Mg.
答案:(μ+cotθ)Mg
14.(12分)为了测量某住宅大楼每层的平均高度(层高)及电梯运行情况,甲、乙两位同学在
一楼电梯内用电子体重计及秒表进行了以下实验.质量为m=50 kg的甲同学站在体重
计上,乙同学记录电梯从地面一楼到顶层全过程中,体重计示数随时间变化的情况,
并作出了如图17所示的图象,已知t=0时,电梯静止不动,从电梯内楼层按钮上获知
该大楼共19层.g取10 m/s2,求:

图17
(1)电梯启动和制动的加速度大小.
(2)电梯上升的总高度及该大楼的层高.
解析:(1)由图可知,第3 s内电梯加速度
由FN1-mg=ma1,可得:a1=2 m/s2
第30 s内电梯加速度
由mg-FN2=ma2,可得a2=2 m/s2.
(2)电梯上升的总高度
H=a1t12+a2t22+a1t1·t匀
=×2×12 m+×2×12 m+2×1×26 m
=54 m
故平均层高为h== m=3 m.
答案:(1)2 m/s2 2 m/s2 (2)54 m 3 m
12.(13分)(2009·江苏高考)“探究加速度与物体质量、物体受力的关系”的实验装置如图13
所示.
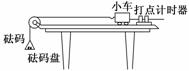
图13
(1)在平衡小车与桌面之间摩擦力的过程中,打出了一条纸带如图14所示.计时器打点
的时间间隔为0.02 s.从比较清晰的点起,每5个点取一个计数点,量出相邻计数点之
间的距离.该小车的加速度a=______m/s2.(结果保留两位有效数字)

图14
(2)平衡摩擦力后,将5个相同的砝码都放在小车上.挂上砝码盘,然后每次从小车上取
一个砝码添加到砝码盘中,测量小车的加速度.小车的加速度a与砝码盘中砝码总重力
F的实验数据如下表:
|
砝码盘中砝 码总重力F(N) |
0.196 |
0.392 |
0.588 |
0.784 |
0.980 |
|
加速度a(m·s-2) |
0.69 |
1.18 |
1.66 |
2.18 |
2.70 |
请根据实验数据在图15中作出a-F的关系图象.

图15
(3)根据提供的实验数据作出的a-F图线不通过原点.请说明主要原因.
解析:(1)a== m/s2=0.16 m/s2或a== m/s2
=0.15 m/s2.
(3)小车、砝码盘和砝码组成的系统所受合外力为砝码盘和砝码的总重力,而表中数据漏
计了砝码盘的重力,导致合力F的测量值小于真实值,a-F的图线不过原点.
答案:(1)0.16(0.15也算对) (2)如下图所示
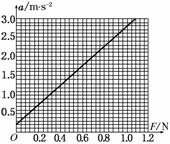
(3)未计入砝码盘的重力
11.(5分)如图12所示为“探究加速度与物体质量、物体受力的关系”的实验中用打点计
时器打出的一条较理想的纸带,纸带上A、B、C、D、E、F、G为七个相邻的计数点,
相邻计数点间的时间间隔是0.1 s,距离如图,单位是cm,小车的加速度是________m/s2.
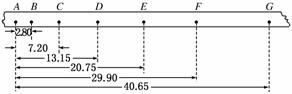
图12
解析:a的计算利用逐差法.
a=
=
=
=×10-2m/s2
=1.60 m/s2
答案:1.60
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com