
3、(2009广东揭阳)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为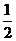 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数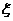 的分布列和数学期望.
的分布列和数学期望.
2、(2009广州(一)某同学如图所示的圆形靶投掷飞镖,飞镖落在靶外(环数记为0)的概率为0.1,飞镖落在靶内的各个点是椭机的.已知圆形靶中三个圆为同心圆,半径分别为30cm、20cm、10cm,飞镖落在不同区域的环数如图中标示.设这位同学投掷一次一次得到的环数这个随机变量x,求x的分布列及数学期望.
1、(2009广州海珠)某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(Ⅰ)试求选出的3种商品中至少有一种是日用商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为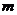 的奖金.假设顾客每次抽奖时获奖与否的概率都是
的奖金.假设顾客每次抽奖时获奖与否的概率都是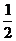 ,请问:商场应将每次中奖奖金数额
,请问:商场应将每次中奖奖金数额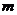 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?

4、(2009惠州)若以连续抛掷两次骰子分别得到的点数m、n作为点P的坐标,则点P落在圆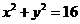 内的概率为( )B
内的概率为( )B
A.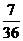 B.
B. 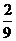 C.
C.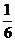 D.
D.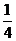
3、(2009番禺)设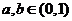 ,则关于
,则关于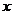 的方程
的方程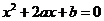 在
在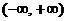 上有两个零点的概率为( )B
上有两个零点的概率为( )B
A. 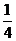 B.
B.  C.
C. 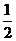 D.
D. 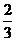
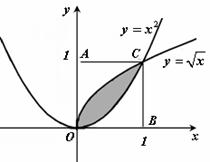
2、(2009广东五校)如图所示,在一个边长为1的正方形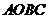 内,曲线
内,曲线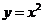 和曲线
和曲线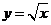 围成一个叶形图(阴影部分),向正方形
围成一个叶形图(阴影部分),向正方形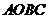 内随机投一点(该点落在正方形
内随机投一点(该点落在正方形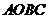 内任何一点是等可能的),则所投的点落在叶形图内部的概率是( )B
内任何一点是等可能的),则所投的点落在叶形图内部的概率是( )B
 (A)
(A)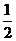 (B)
(B)
(C)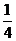 (D)
(D)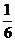
1、(2009揭阳)已知函数: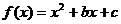 ,其中:
,其中: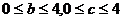 ,记函数
,记函数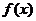 满足条件:
满足条件: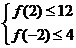 为事件为A,则事件A发生的概率为( )C
为事件为A,则事件A发生的概率为( )C
A. 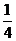 B.
B. 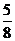 C.
C. 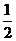 D.
D. 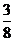
12、解:(1)由于点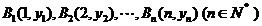 在直线
在直线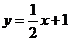 上,
上,
则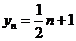 ,
……1分
,
……1分
因此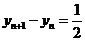 ,所以数列
,所以数列 是等差数列 ……2分
是等差数列 ……2分
(2)由已知有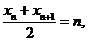 ,那么
,那么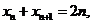 ……3分
……3分
同理
以上两式相减,得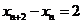 ,
……4分
,
……4分
∴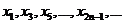 成等差数列;
成等差数列;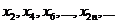 也成等差数列,
也成等差数列,
∴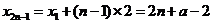 ,
……5分
,
……5分
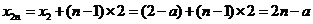 ……6分
……6分
点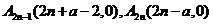 ,则
,则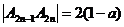 ,
,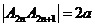 ,
,
而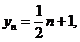
∴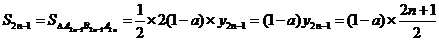 ……8分
……8分
(3)由(1)得: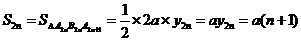 , ……9分
, ……9分
则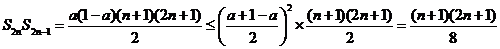
而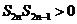 ,则
,则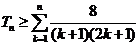 ,
……11分
,
……11分
即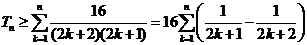
∴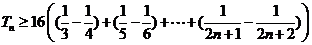
∴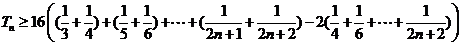
∴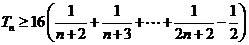 ……12分
……12分
由于
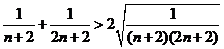 ,
,
而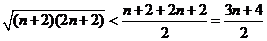 ,
,
则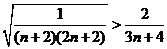 , 从而
, 从而 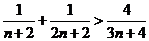 , ……13分
, ……13分
同理: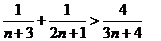
……
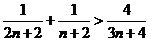
以上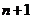 个不等式相加得:
个不等式相加得:
即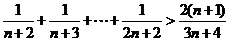 ,
,
从而
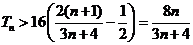 ……14分
……14分
说明:(1)也可由数学归纳法证明  ;
;
(2)本题也可以求出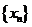 的通项公式,由
的通项公式,由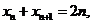 两边同时除以
两边同时除以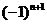 ,
,
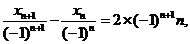
令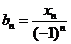 ,则
,则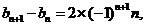
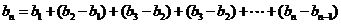
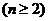
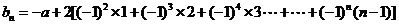
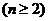
利用错位相减法可求出:

则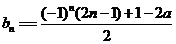 ,
,
则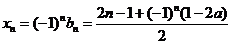 ,
,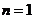 时,也符合上式,
时,也符合上式,
则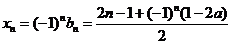 对任意正整数
对任意正整数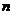 都成立.
都成立.
下同上述解法
10、解:(Ⅰ)由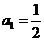 ,
,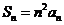 ,
①
,
①
∴
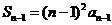 ,
②
,
②
①-②得: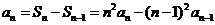 ,即
,即
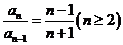 ,
4分
,
4分
∵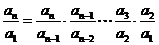
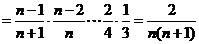 ,
,
∴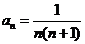 。
8分
。
8分
(Ⅱ)∵ ,∴
,∴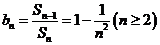 ,
10分
,
10分
∴ 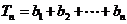
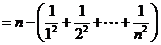
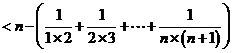
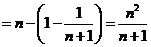 .
.
故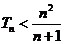 .
14分
.
14分
9、解:(1)
解法一:由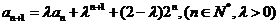 ,可得
,可得
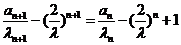 ………………………………2分
………………………………2分
所以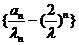 是首项为0,公差为1的等差数列.
是首项为0,公差为1的等差数列.
所以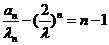 即
即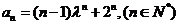 ……………………4分
……………………4分
解法二:因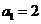 且
且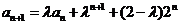 得
得
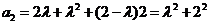 ,
,
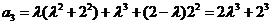 ,
,
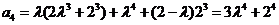 ,
,
…………………………………………………………
由此可猜想数列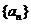 的通项公式为:
的通项公式为: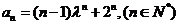 …………2分
…………2分
以下用数学归纳法证明:
①当n=1时,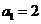 ,等式成立;
,等式成立;
②假设当n=k时,有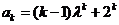 成立,那么当n=k+1时,
成立,那么当n=k+1时,
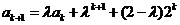
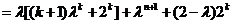
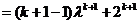 成立
成立
所以,对于任意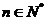 ,都有
,都有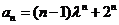 成立……………………4分
成立……………………4分
(2)解:设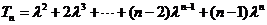 ……①
……①
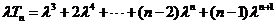 ……②
……②
当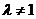 时,①
时,①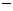 ②得
②得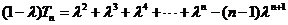
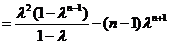
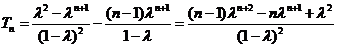 …………6分
…………6分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com