
8、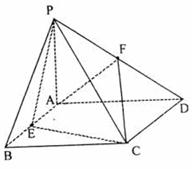 (2009广州(一))如图,四棱锥
(2009广州(一))如图,四棱锥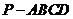 中,
中,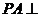 平面
平面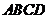 ,四边形
,四边形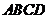 是矩形,
是矩形,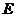 、
、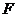 分别是
分别是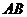 、
、 的中点.若
的中点.若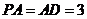 ,
,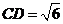 .
.
(Ⅰ)求证: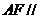 平面
平面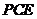 ;
;
(Ⅱ) 求点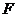 到平面
到平面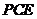 的距离;
的距离;
(Ⅲ)求直线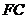 平面
平面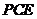 所成角的正弦值.
所成角的正弦值.
7、(2009广州海珠)如图6,在直角梯形ABCP中,AP//BC,AP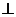 AB,AB=BC=
AB,AB=BC=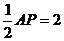 ,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将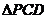 沿CD折起,使得
沿CD折起,使得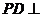 平面ABCD,如图7.
平面ABCD,如图7.
(Ⅰ)求证:AP//平面EFG;
(Ⅱ) 求二面角 的大小;
的大小;
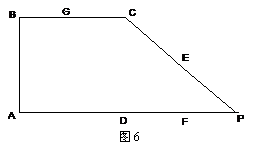 (Ⅲ)求三棱椎
(Ⅲ)求三棱椎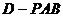 的体积.
的体积.

6、(2009广东东莞)在直三棱柱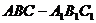 中,
中,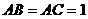 ,
,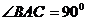 ,且异面直线
,且异面直线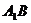 与
与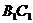 所成的角等于
所成的角等于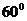 ,设
,设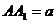 .
.
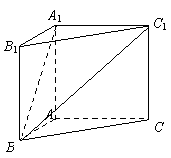 (1)求
(1)求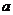 的值;
的值;
(2)求平面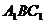 与平面
与平面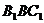 所成的锐二面角的大小.
所成的锐二面角的大小.
5、(09北江中学文期末)如图,在底面是矩形的四棱锥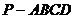 中,
中,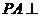 面
面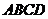 ,
,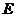 、
、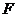 为别为
为别为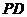 、
、
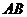 的中点,且
的中点,且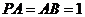 ,
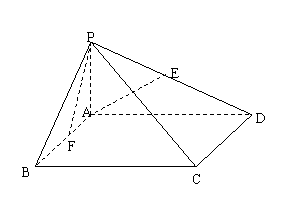
,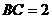 ,
,
(Ⅰ)求四棱锥 的体积;
的体积;
 (Ⅱ)求证:直线
(Ⅱ)求证:直线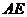 ∥平面
∥平面
3、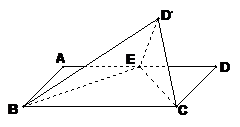 (09广东四校理期末)如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
(09广东四校理期末)如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
(1)证明:BE⊥C D′;
(2)求二面角D′-BC-E的正切值.
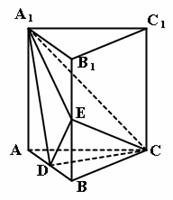
4(09广东四校文期末)如图:直三棱柱ABC-A1B1C1中, AC=BC=AA1=2,∠ACB=90°.E为BB1的中点,D点在AB上且DE=.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求三棱锥A1-CDE的体积.
2、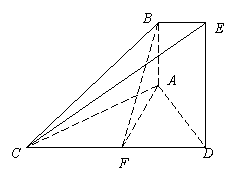 (2009广雅期中)如图,已知
(2009广雅期中)如图,已知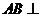 平面
平面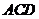 ,
, 平面
平面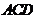 ,△
,△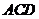 为等边三角形,
为等边三角形,
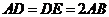 ,
,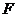 为
为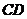 的中点.
的中点.
(1) 求证: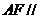 平面
平面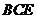 ;
;
(2) 求证:平面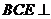 平面
平面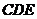 ;
;
(3) 求直线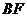 和平面
和平面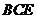 所成角的正弦值.
所成角的正弦值.
1、(2009广雅期中)已知四棱锥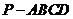 的三视图如下图所示,
的三视图如下图所示,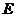 是侧棱
是侧棱 上的动点.
上的动点.
(1) 求四棱锥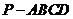 的体积;
的体积;
(2) 是否不论点 在何位置,都有
在何位置,都有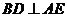 ?证明你的结论;
?证明你的结论;
(3) 若点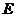 为
为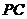 的中点,求二面角
的中点,求二面角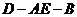 的大小.
的大小.

10、(2009韶关田家炳)设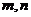 是两条不同的直线,
是两条不同的直线,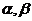 是两个不同的平面,下列命题中,其中正确的命题是( )
是两个不同的平面,下列命题中,其中正确的命题是( )
A. 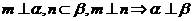 B.
B. 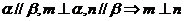
C. 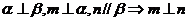 D.
D.
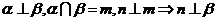
9、(2009澄海)设m,n是两条不同的直线,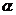 ,
,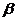 ,
,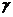 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若m⊥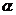 ,n∥
,n∥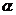 ,则m⊥n;
,则m⊥n;
②若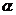 ∥
∥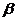 ,
,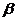 ∥
∥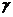 ,m⊥
,m⊥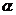 ,则m⊥
,则m⊥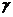 ;
;
③若m∥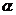 ,n∥
,n∥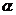 ,则m∥n;
,则m∥n;
④若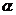 ⊥
⊥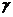 ,
,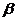 ⊥
⊥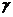 ,则
,则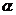 ∥
∥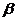 .
.
其中正确命题的序号是( )A
A.①和② B.②和③ C.③和④ D.①和④
8、(2009潮州)设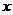 、
、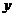 、
、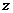 是空间不同的直线或平面,对下列四种情形:
是空间不同的直线或平面,对下列四种情形:
① 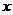 、
、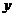 、
、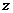 均为直线;②
均为直线;② 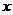 、
、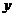 是直线,
是直线,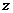 是平面;③
是平面;③ 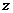 是直线,
是直线,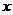 、
、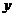 是平面;④
是平面;④ 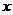 、
、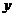 、
、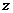 均为平面。
均为平面。
其中使“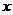 ⊥
⊥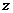 且
且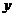 ⊥
⊥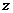

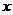 ∥
∥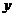 ”为真命题的是 ( )C
”为真命题的是 ( )C
A ③ ④ B ① ③ C ② ③ D ① ②
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com