
5.一次、二次不等式组成的不等式组仍要借助于数轴.
4.注意必要的讨论.
3.一次不等式,二次不等式,特殊的高次不等式及分式不等式,我们称之为有理不等式.
2.分式不等式,切忌去分母,一律移项通分化为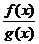 >0(或
>0(或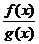 <0)的形式,转化为:
<0)的形式,转化为: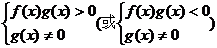 ,即转化
,即转化
为一次、二次或特殊高次不等式形式 .
也可以直接用根轴法(零点分段法)求解
1.特殊的高次不等式即右边化为0,左边可分解为一次或二次式的因式的形式不等式,一般用区间法解,注意:①左边各因式中x的系数化为“+”,若有因式为二次的(不能再分解了)二次项系数也化为“+”,再按我们总结的规律作;②注意边界点(数轴上表示时是“0”还是“.”).
⒈ 一元二次不等式与特殊的高次不等式解法
例1 解不等式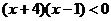 .
.
分析一:利用前节的方法求解;
分析二:由乘法运算的符号法则可知,若原不等式成立,则左边两个因式必须异号,∴原不等式的解集是下面两个不等式组: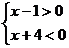 与
与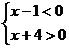 的解集的并集,即{x|
的解集的并集,即{x|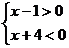 }∪
}∪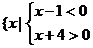 }=φ∪{x|-4<x<1}={x|-4<x<1}.书写时可按下列格式:
}=φ∪{x|-4<x<1}={x|-4<x<1}.书写时可按下列格式:
解二:∵(x-1)(x+4)<0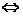
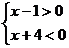 或
或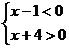
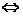 x∈φ或-4<x<1
x∈φ或-4<x<1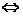 -4<x<1,
-4<x<1,
∴原不等式的解集是{x|-4<x<1}.
小结:
一元二次不等式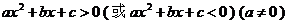 的代数解法:设一元二次不等式
的代数解法:设一元二次不等式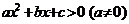 相应的方程
相应的方程
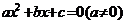 的两根为
的两根为 ,
,
则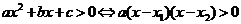 ;
;
①若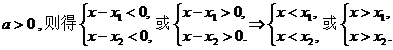
当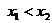 时,得
时,得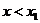 或
或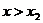 ;当
;当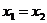 时,得
时,得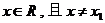 .
.
②若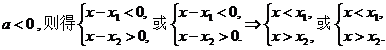
当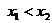 时,得
时,得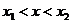 ;当
;当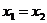 时,得
时,得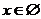 .
.
分析三:由于不等式的解与相应方程的根有关系,因此可求其根并由相应的函数值的符号表示出来即可求出不等式的解集.
解:①求根:令(x-1)(x+4)=0,解得x(从小到大排列)分别为-4,1,这两根将x轴分为三部分:(-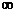 ,-4)(-4,1)(1,+
,-4)(-4,1)(1,+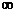 );
);
②分析这三部分中原不等式左边各因式的符号
|
|
(-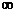 ,-4) ,-4) |
(-4,1) |
(1,+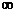 ) ) |
|
x+4 |
- |
+ |
+ |
|
x-1 |
- |
- |
+ |
|
(x-1)(x+4) |
+ |
- |
+ |
③由上表可知,原不等式的解集是{x|-4<x<1}.
例2:解不等式:(x-1)(x+2)(x-3)>0;
解:①检查各因式中x的符号均正;
②求得相应方程的根为:-2,1,3;
③列表如下:
|
|
-2 1 3 |
|||
|
x+2 |
- |
+ |
+ |
+ |
|
x-1 |
- |
- |
+ |
+ |
|
x-3 |
- |
- |
- |
+ |
|
各因式积 |
- |
+ |
- |
+ |
④由上表可知,原不等式的解集为:{x|-2<x<1或x>3}.
小结:此法叫列表法,解题步骤是:
①将不等式化为(x-x1)(x-x2)…(x-xn)>0(<0)形式(各项x的符号化“+”),令(x-x1)(x-x2)…(x-xn)=0,求出各根,不妨称之为分界点,一个分界点把(实数)数轴分成两部分,n个分界点把数轴分成n+1部分……;
②按各根把实数分成的n+1部分,由小到大横向排列,相应各因式纵向排列(由对应较小根的因式开始依次自上而下排列);
③计算各区间内各因式的符号,下面是乘积的符号;
④看下面积的符号写出不等式的解集.
练习:解不等式:x(x-3)(2-x)(x+1)>0. {x|-1<x<0或2<x<3}.
 思考:由函数、方程、不等式的关系,能否作出函数图像求解
思考:由函数、方程、不等式的关系,能否作出函数图像求解
直接写出解集:{x|-2<x<1或x>3}. {x|-1<x<0或2<x<3}
在没有技术的情况下:
可大致画出函数图形求解,称之为根轴法(零点分段法)
①将不等式化为(x-x1)(x-x2)…(x-xn)>0(<0)形式,并将各因式x的系数化“+”;(为了统一方便)
②求根,并在数轴上表示出来;
③由右上方穿线,经过数轴上表示各根的点(为什么?);
④若不等式(x的系数化“+”后)是“>0”,则找“线”在x轴上方的区间;若不等式是“<0”,则找“线”在x轴下方的区间.

注意:奇过偶不过
例3 解不等式:(x-2)2(x-3)3(x+1)<0.
解:①检查各因式中x的符号均正;
②求得相应方程的根为:-1,2,3(注意:2是二重根,3是三重根);
③在数轴上表示各根并穿线,每个根穿一次(自右上方开始奇过偶不过),如下图: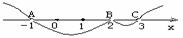
④∴原不等式的解集为:{x|-1<x<2或2<x<3}.
说明:∵3是三重根,∴在C处过三次,2是二重根,∴在B处过两次,结果相当于没过.由此看出,当左侧f(x)有相同因式(x-x1)n时,n为奇数时,曲线在x1点处穿过数轴;n为偶数时,曲线在x1点处不穿过数轴,不妨归纳为“奇过偶不过”.
练习:解不等式:(x-3)(x+1)(x2+4x+4)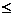 0.
0.
解:①将原不等式化为:(x-3)(x+1)(x+2)2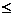 0;
0;
②求得相应方程的根为:-2(二重),-1,3;
③在数轴上表示各根并穿线,如图:
④∴原不等式的解集是{x|-1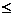 x
x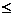 3或x=-2}.
3或x=-2}.
说明:注意不等式若带“=”号,点画为实心,解集边界处应有等号;另外,线虽不穿过-2点,但x=-2满足“=”的条件,不能漏掉.
2.分式不等式的解法
例4 解不等式: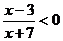 .
.
错解:去分母得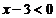 ∴原不等式的解集是
∴原不等式的解集是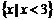 .
.
解法1:化为两个不等式组来解:
∵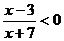
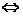
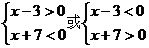
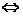 x∈φ或
x∈φ或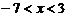
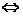
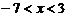 ,
,
∴原不等式的解集是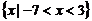 .
.
解法2:化为二次不等式来解:
∵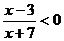
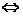
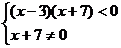
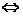
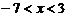 ,
,
∴原不等式的解集是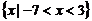
说明:若本题带“=”,即(x-3)(x+7)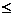 0,则不等式解集中应注意x
0,则不等式解集中应注意x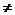 -7的条件,解集应是{x| -7<x
-7的条件,解集应是{x| -7<x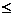 3}.
3}.
小结:由不等式的性质易知:不等式两边同乘以正数,不等号方向不变;不等式两边同乘以负数,不等号方向要变;分母中有未知数x,不等式两边同乘以一个含x的式子,它的正负不知,不等号方向无法确定,无从解起,若讨论分母的正负,再解也可以,但太复杂.因此,解分式不等式,切忌去分母.
解法是:移项,通分,右边化为0,左边化为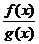 的形式.
的形式.
例5 解不等式: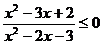 .
.
解法1:化为不等式组来解较繁.
解法2:∵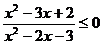
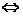
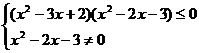
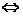
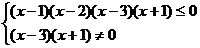 ,
,
∴原不等式的解集为{x| -1<x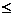 1或2
1或2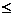 x<3}.
x<3}.
也可以直接用根轴法(零点分段法)求解: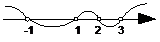
练习:1.课本P21练习:3⑴⑵;2.解不等式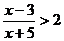 .
.
答案:1.⑴{x|-5<x<8};⑵{x|x<-4,或x>-1/2};2.{x|-13<x<-5}.
2解不等式: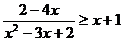 .(答:{x|x
.(答:{x|x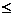 0或1<x<2})
0或1<x<2})
2.一元二次不等式的解法步骤
一元二次不等式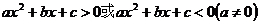 的解集:
的解集:
设相应的一元二次方程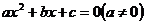 的两根为
的两根为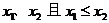 ,
,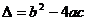 ,则不等式的解的各种情况如下表:(课本第19页)
,则不等式的解的各种情况如下表:(课本第19页)
|
|
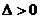 |
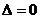 |
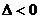 |
|
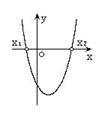
二次函数 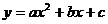 (  )的图象 )的图象 |
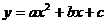  |
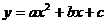 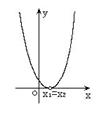 |
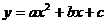 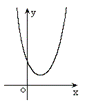 |
一元二次方程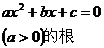 |
有两相异实根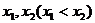 |
有两相等实根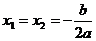 |
无实根 |
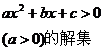 |
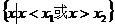 |
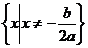 |
R |
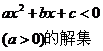 |
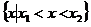 |
 |
 |
引言:今天我们来研究一元二次不等式的另外解法,以及特殊的高次不等式、分式不等式的解法
1.一元二次方程、一元二次不等式与二次函数的关系
32.(6分)有研究小组通过洋葱根尖分生区有丝分裂实验,比较一个细胞周期中不同时期的长短,又根据细胞周期时间长短计算某个时期的细胞数,获得了表一所示的实验数据。
表一 洋葱根尖有丝分裂细胞周期中不同时期的细胞数
|
细胞周期 |
间 期 |
分裂期 |
||
|
前期 |
中期 |
后期和末期 |
||
|
实验小组1计数细胞个数 |
43 |
4 |
1 |
2 |
|
实验小组2计数细胞个数 |
44 |
3 |
0 |
3 |
|
…… |
…… |
…… |
…… |
…… |
|
全班计数细胞个数 |
880 |
67 |
18 |
35 |
|
计数细胞总数 |
1000 |
通过有关动物细胞培养实验获得B图所示实验数据,B图表示处于一个细胞周期中
各个时期细胞数目的变化(用特殊的方法在一个培养基中测得的),A图表示在一个细
胞周期(G1、S、G2组成了分裂间期,M为分裂期)中的细胞核内DNA含量的变化曲
线。请根据表和图中的信息回答下列问题:
(1)若已知洋葱根尖分生区有丝分裂的细胞周期为12 h,根据实验数据,计算分裂间期的时间约为 h(保留1位小数);分裂前期细胞的主要特征是 。
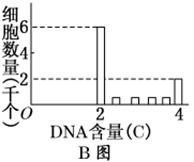
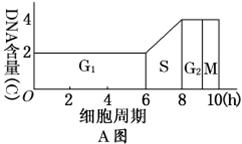 (2)根据B图,DNA含量为4C的细胞,处在A图的 期。用DNA合成抑制剂处理,B图中DNA含量为2C的细胞数量会 。用秋水仙素处理,B图中DNA含量为 C的细胞数量会增加。根据A、B图示信息,S期细胞数是 个。
(2)根据B图,DNA含量为4C的细胞,处在A图的 期。用DNA合成抑制剂处理,B图中DNA含量为2C的细胞数量会 。用秋水仙素处理,B图中DNA含量为 C的细胞数量会增加。根据A、B图示信息,S期细胞数是 个。
31..(8分)将长势相同、数量相等的甲、乙两个品种的大豆幼苗分别置于两个相同的密闭透明玻璃罩内,在光照、温度等相同且适宜的条件下培养,定时测定玻璃罩内的CO2含量,结果如图。据图回答:
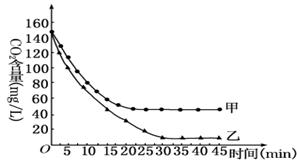
(1)0-25 min期间,影响甲品种大豆幼苗光合作用强度的主要因素是 含量。
(2)乙植株比甲植株固定CO2的能力 。
(3)0-15 min期间植株释放O2速率的变化趋势是 。
(4)30-45min期间两个玻璃罩内CO2含量相对稳定的原因是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com