
两年高考·精选(2008-2009)
考点1 基本概念的理解
1.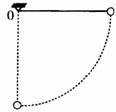 (09·广东文科基础·58) 如图8所示,用一轻绳系一小球悬于O点。现将小球拉至水 平位置,然后释放,不计阻力。小球下落到最低点的过程中,下列表述正确的是 ( A )
(09·广东文科基础·58) 如图8所示,用一轻绳系一小球悬于O点。现将小球拉至水 平位置,然后释放,不计阻力。小球下落到最低点的过程中,下列表述正确的是 ( A )
A.小球的机械能守恒
B.小球所受的合力不变
C.小球的动能不断减小
D.小球的重力势能增加
(七)教学设计
1.情境设置生活化.
本着新课程的教学理念,考虑到高一学生的心理特点以及初、高中教学的衔接,让学生学生初步了解“数学来源于生活”,引入材料源于历史,通过创设问题情景,意在营造和谐、积极的学习气氛,激发学生的探究欲.
2.问题探究活动化.
教学中本着以学生发展为本的理念,充分给学生想的时间、说的机会以及展示思维过程的舞台,通过他们自主学习、合作探究,展示学生解决问题的思想方法,共享学习成果,体验数学学习成功的喜悦.通过师生之间不断合作和交流,发展学生的数学观察能力和语言表达能力,培养学生思维的发散性和严谨性.
3.辨析质疑结构化.
在理解公式的基础上,及时进行正反两方面的“短、平、快”填空练习.通过总结、辨析和反思,强化了公式的结构特征,促进学生主动建构,有助于学生形成知识模块,优化知识体系.
4.思路拓广数学化.
从整理知识提升到强化方法,由课内巩固延伸到课外思考,变“知识本位”为“学生本位”,使数学学习成为提高学生素质的有效途径.以生活中的实例作为思考,让学生认识到数学来源于生活并应用于生活,生活中处处有数学.
6.作业布置弹性化.
通过布置弹性作业,为学有余力的学生提供进一步发展的空间.
备用
南北朝时,张丘建始创等差数列求和解法。他在《张丘建算经》里给出了几个等差数列问题。 例如:“今有女子不善织布,逐日所织的布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?”
原书的解法是:“并初、末日织布数,半之,余以乘织讫日数,即得。”
再如:“今有女子善织布,逐日所织的布以同数递增,初日织五尺,计织三十日,共织九匹三丈,问日增几何?”
(七)板书设计
(六)布置作业
A必做题:课本118页,习题3.3第2题(3、4)
B选做题:在等差数列中
1等差数列前n项和公式
2公式的推证用的是倒序相加法
3在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.(体现了 方程思想)
1姚明刚进NBA一周训练罚球的个数:
第一天:600, 第二天:650,第三天:700, 第四天:750,
第五天:800, 第六天:850,第七天:900.
求:他一周训练罚球的总个数?
2求正整数列中前n个偶数的和.
3. 等差数列 5,4,3,2, ··· 前多少项和是 –30?
例1如图,一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放1支,最上面一层放120支. 这个V形架上共放了多少支铅笔?
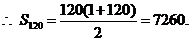 解:由题意知,这个V型架自下而上是个由120层的铅笔构成的等差数列,记为{an},
解:由题意知,这个V型架自下而上是个由120层的铅笔构成的等差数列,记为{an},
答:V型架上共放着7260支铅笔
例2:等差数列-10,-6,-2,2,·······
(1)求其前100项和
(2)前多少项和是54 ?
(3)你能根据本题提供的等差数列自拟几道求和问题吗?
解:设题中的等差数列为{an}
注:1应用公式时,要根据题目的具体条件,灵活选取这两个公式 )
2 在等差数列的求和公式中,含有四个量,运用方程的思想,知三可求一.
1建筑工地上一堆圆木,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根圆木?如何用简便的方法

三探究发现
变式:
问题1若把问题变成求:1+2+3+4+‥ ‥ +99=?可以用哪些方法求出来呢?
方法1:原式=(1+2+3+4+‥ ‥ +99+100)-100
方法2:原式=(1+2+3+4+‥ ‥ +98)+99
方法3:原式=0+1+2+3+4+‥ ‥ +98+99
方法4:原式=(1+2+3+4+‥ +49+51+52+‥ 99)+50
方法5:原式=(1+2+3+4+‥ ‥ +98+99+99+98+‥ +2+1)÷ 2
方法6 令 S=1+2+3+4+‥ ‥ +99
又 S=99+98+97+‥ +2+1
故 2S=(1+99)+(2+98)+‥ ‥ +(98+2)+(99+1) 从而 S =(100×99)÷ 2 = 4950
问题2:1+2+3+4+‥ ‥ +(n-1)+n=? 在上面6种方法中,哪个能较好地推广应用于这个式子的求和?
令 Sn =1+2+3+4+‥ ‥ +n,
则 Sn =n+(n-1)+‥ ‥ +2+1
从而有
2Sn =(n+1) + (n+1) + (n+1) +‥ ‥ +(n+1)
=(n+1)n

上述求解过程带给我们什么启示?
(1)所求的和可以用首项、末项及项数来表示;
(2)等差数列中任意的第k项与倒数第k项的和都等于首项与末项的和。
问题 3:现在把问题推广到更一般的情形:
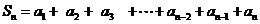 设数列 {an }为等差数列,它的首项为a1
, 公差为d, 试求 Sn =a1 +a2 + a3 +‥ ‥ + an-1 +an
设数列 {an }为等差数列,它的首项为a1
, 公差为d, 试求 Sn =a1 +a2 + a3 +‥ ‥ + an-1 +an
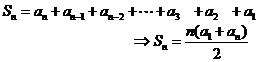
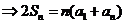 (I)
(I)
an=a1+(n-1)d代入公式(1)得
Sn=na1+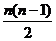 d(II)
d(II)
等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表:
|
a1 |
d |
n |
an |
sn |
|
5 |
10 |
10 |
|
|
|
|
-2 |
50 |
|
2550 |
|
-38 |
|
|
-10 |
-360 |
|
14.5 |
|
26 |
32 |
|
说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。
4. (1)求函数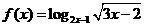 的定义域.
的定义域.
(2)求函数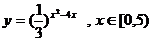 的值域.
的值域.
3. 已知函数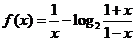 ,求函数的定义域,并讨论它的奇偶性单调性.
,求函数的定义域,并讨论它的奇偶性单调性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com