
6.已知sin(a+b) =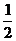 ,sin(a-b) =
,sin(a-b) = ,求
,求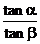 的值
的值
解:由题设: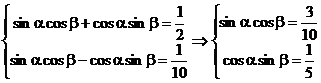
从而 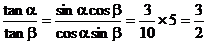
或设:x
=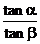 ∵
∵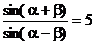
∴
∴x
=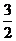 即
即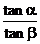 =
=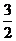
5.设a,bÎ(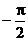 ,
,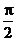 ),tana、tanb是一元二次方程
),tana、tanb是一元二次方程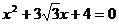 的两个根,求 a + b
的两个根,求 a + b
解:由韦达定理:
∴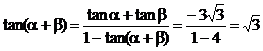
又由a,bÎ(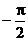 ,
,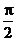 )且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
)且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
得a + bÎ (-p, 0) ∴a + b = 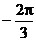
4.已知sina +
sinb = 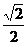 ,求cosa + cosb的范围
,求cosa + cosb的范围
解:设cosa + cosb = t,
则(sina + sinb)2 + (cosa +
cosb)2 = 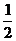 + t2
+ t2
∴2
+ 2cos(a - b) = 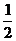 + t2
+ t2
即
cos(a - b) = 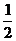 t2 -
t2 -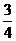
又∵-1≤cos(a - b)≤1 ∴-1≤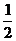 t2 -
t2 -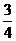 ≤1
≤1
∴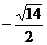 ≤t≤
≤t≤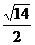
3.已知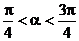 ,
, ,
,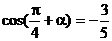 ,
,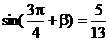 ,
,
求sin(a + b)的值
解:∵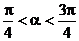 ∴
∴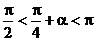
又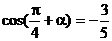 ∴
∴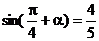
∵ ∴
∴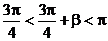
又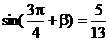 ∴
∴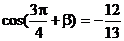
∴sin(a + b) = -sin[p + (a + b)] = 
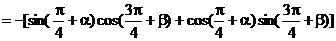
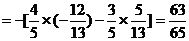
2.在△ABC中,ÐC>90°,则tanAtanB与1的关系适合………………(B)
A tanAtanB>1 B
tanAtanB>1 B tanAtanB>1 C
tanAtanB>1 C tanAtanB =1 D
tanAtanB =1 D 不确定
不确定
解:在△ABC中 ∵ÐC>90° ∴A, B为锐角 即tanA>0, tanB>0
又:tanC<0 于是:tanC
= -tan(A+B) = 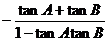 <0
<0
 ∴1 - tanAtanB>0 即:tanAtanB<1
∴1 - tanAtanB>0 即:tanAtanB<1
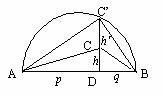
又解:在△ABC中 ∵ÐC>90°
∴C必在以AB为直径的⊙O内(如图)
过C作CD^AB于D,DC交⊙O于C’,
设CD = h,C’D = h’,AD = p,BD = q,
则tanAtanB
1.在△ABC中,已知cosA =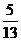 ,sinB =
,sinB =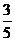 ,则cosC的值为…………(A)
,则cosC的值为…………(A)
A
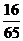 B
B
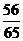 C
C
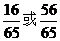 D
D
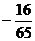
解:∵C = p - (A + B) ∴cosC = - cos(A + B)
又∵AÎ(0, p) ∴sinA = 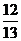 而sinB =
而sinB =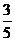 显然sinA > sinB
显然sinA > sinB
∴A
> B 即B必为锐角 ∴ cosB = 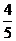
∴cosC
= - cos(A + B) = sinAsinB -
cosAcosB =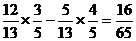
例1 1°用反三角函数表示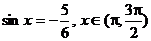 中的角x
中的角x
2°用反三角函数表示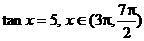 中的角x
中的角x
解:1° ∵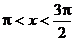 ∴
∴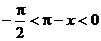
又由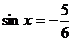 得
得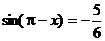
∴ ∴
∴
2° ∵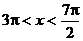 ∴
∴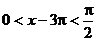
又由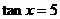 得
得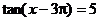
∴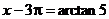 ∴
∴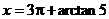
例2 已知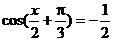 ,求角x的集合
,求角x的集合
解:∵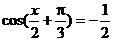 ∴
∴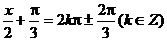
由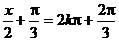 得
得 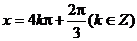
由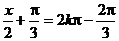 得
得 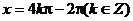
故角x的集合为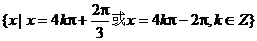
例3 求 的值
的值
解:arctan2 = a, arctan3 = b 则tana = 2, tanb = 3
且 ,
, 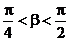
∴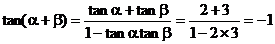
而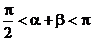 ∴a + b =
∴a + b = 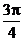
又arctan1
= 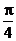 ∴
∴ = p
= p
例4求y = arccos(sinx), (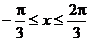 )的值域
)的值域
解:设u = sin x ∵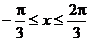 ∴
∴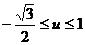
∴ ∴所求函数的值域为
∴所求函数的值域为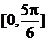
例5设xÎ[0,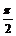 ], f (x)=sin(cosx), g (x)=cos(sinx) 求f (x)和g (x)的最大值和最小值,并将它们按大小顺序排列起来
], f (x)=sin(cosx), g (x)=cos(sinx) 求f (x)和g (x)的最大值和最小值,并将它们按大小顺序排列起来
解:∵在[0,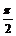 ]上y=cosx单调递减, 且cosxÎ[0,1]
在此区间内y=sinx单调递增且sinxÎ[0,1] ∴f (x)=sin(cosx)Î[0,sin1] 最小值为0,
最大值为sin1
]上y=cosx单调递减, 且cosxÎ[0,1]
在此区间内y=sinx单调递增且sinxÎ[0,1] ∴f (x)=sin(cosx)Î[0,sin1] 最小值为0,
最大值为sin1
g (x)=cos(sinx)Î[cos1,1] 最小值为cos1, 最大值为1
∵cos1=sin(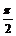 -1)<sin1 ∴它们的顺序为:0<cos1<sin1<1
-1)<sin1 ∴它们的顺序为:0<cos1<sin1<1
例6 已知△ABC的两边a, b ,它们的夹角为C
1°试写出△ABC面积的表达式;
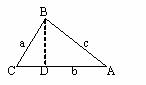 2°当ÐC变化时,求△AABC面积的最大值
2°当ÐC变化时,求△AABC面积的最大值
解:1° 如图:设AC边上的高h=asinC
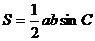
2°当C=90°时[sinC]max=1
∴[S△ABC]max=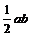
例7 求函数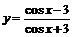 的最大值和最小值
的最大值和最小值
解:(部分分式) 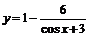
当cosx=1时 ymax=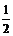 ;当cosx=-1时 ymin= -2
;当cosx=-1时 ymin= -2
例8求函数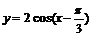 (
(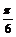 ≤x≤
≤x≤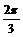 )的最大值和最小值
)的最大值和最小值
解:∵xÎ[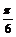 ,
,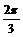 ]
∴x-
]
∴x-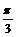 Î[-
Î[-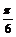 ,
,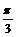 ]
]
∴当x-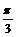 =0 即x=
=0 即x=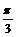 时 ymax=2
时 ymax=2
当x-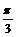 =
=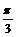 即x=
即x=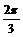 时 ymin=1
时 ymin=1
例9求函数f (x)=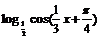 的单调递增区间
的单调递增区间
解:∵f (x)=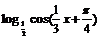
令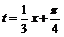 ∴y=
∴y=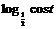 ,t是x的增函数
,t是x的增函数
又∵0<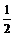 <1
<1
∴当y=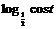 为单调递增时 cost为单调递减 且cost>0
为单调递增时 cost为单调递减 且cost>0
∴2kp≤t<2kp+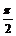 (kÎZ)
(kÎZ)
∴2kp≤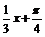 <2kp+
<2kp+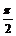 (kÎZ) 6kp-
(kÎZ) 6kp-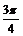 ≤x<6kp+
≤x<6kp+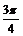 (kÎZ)
(kÎZ)
∴f (x)=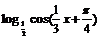 的单调递减区间是[6kp-
的单调递减区间是[6kp-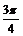 ,6kp+
,6kp+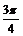 ) (kÎZ)
) (kÎZ)
20.把下列句子组成语意连贯的一段话。(4分,只填序号)
①东岸的风光不同,与西岸形成令人赞叹的对比。
②绿色的波浪逶迤而去,在天际同蓝天连成一片。
③河边,山巅,岩石上,幽谷里,各种颜色,各种芳香的树木杂处一堂,茁壮生长。
④西岸,草原一望无际。
⑤野葡萄,喇叭花,苦苹果在树下交错,在树枝上攀援。
⑥密西西比河岸风光旖旎。
答案
19.森马集团有限公司的一则休闲服宣传广告语“我管不了全球变暖,只要我好看!”一出,无数网民强烈批评它的负面效应,集团负责人却大呼冤枉,认为该广告词有着较为积极的内涵。请分别站在双方的立场上,各用一句话简明准确地分析这则广告语所体现出的含义。(6分)
(1)森马
(2)网
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com