
1.B 2.A 3.C 4.D 5.从属 先后 6.整个系统
[典例精析]
变式训练:
3.环,树
[基础闯关]
2.从上到下 从左到右 从属关系 逻辑的先后关系
1.若干要素 连线(方向箭头)
12. 解:(Ⅰ)∵f(x)的定义域D=(-∞?-1)∪(-1,+∞)
∴数列{xn}只有三项x1=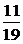 ,x2=
,x2=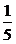 ,x3=-1
,x3=-1
(Ⅱ)∵f(x)=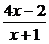 =x即x2-3x+2=0,∴x=1或x=2
=x即x2-3x+2=0,∴x=1或x=2
即x0=1或2时,xn+1=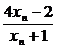 =xn
=xn
故当x0=1时,x0=1;当x0=2时,xn=2(n∈N)
(Ⅲ)解不等式x<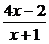 ,得x<-1或1<x<2,
,得x<-1或1<x<2,
要使x1<x2,则x2<-1或1<x1<2
对于函数f(x)=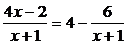
若x1<-1,则x2=f(x1)>4,x3=f(x2)<x2
当1<x1<2时,x2=f(x)>x1且1<x2<2
依次类推可得数列{xn}的所有项均满足xn+1>xn(n∈N)
综上所述,x1∈(1,2),由x1=f(x0),得x0∈(1,2)
第二讲 结构图
[知识梳理]
[知识盘点]
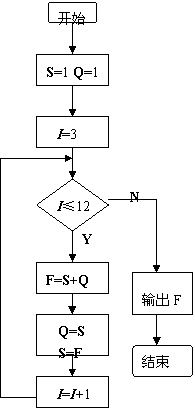
11. 解:根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N个月有两F对兔子,第N-1个月有S对兔子,第N-2个月有Q对兔子,则有F=S+Q,一个月后,即第N+1个月时,式中变量S的新值应变第N个月兔子的对数(F的旧值),变量Q的新值应变为第N-1个月兔子的对数(S的旧值),这样,用S+Q求出变量F的新值就是N+1个月兔子的数,依此类推,可以得到一个数序列,数序列的第12项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,让表示“第×个月的I从3逐次增加1,一直变化到12,最后一次循环得到的F”就是所求结果. 流程图如右图所示:
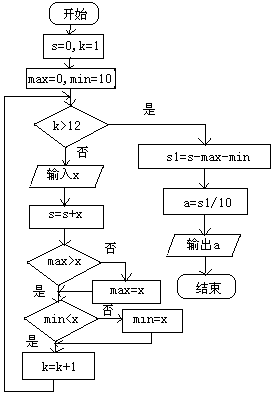
10.解:由于共有12位评委,所以每位选手会有12个分数,我们可以用循环语句来完成这12个分数的输入,同时设计累加变量求出这12个分数的和,本问题的关键在于从这12个输入分数中找出最大数与最小数,以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间,去我们可以先假设其中的最大数为0,最小数为10,然后每次输入一个评委的分数,就进行一次比较,若输入的数大于0,就将之代替最大数,若输入的数小于10,就用它代替最小数,依次下去,就能找出这12个数中的最大数与最小数,循环结束后,从总和中减去最大数与最小数,再除以10,就得到该选手最后的平均数.
 程序框图如图所示.
程序框图如图所示.
8.流程线 9.2
1.B 2.C 3.A 4.B 5.B 6.n-2 7.顺序 条件(选择) 循环
6.解:
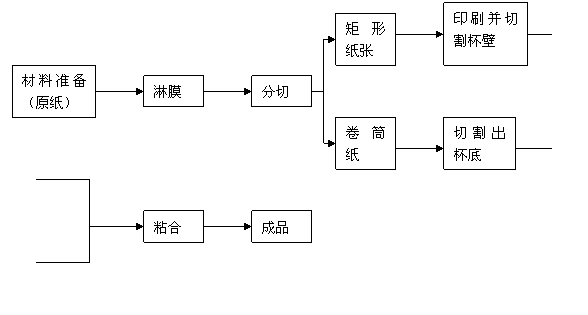

[能力提升]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com