
用韦达定理解“含参二次方程的实根分布”问题的基本方法
2.若方程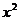 -(k+2)x+4=0有两负根,求k的取值范围.
-(k+2)x+4=0有两负根,求k的取值范围.
提示:由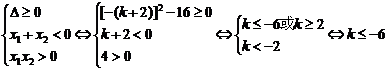 .
.
1.关于x的方程m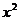 +(2m+1)x+m=0有两个不等的实根,则m的取值范围是:
+(2m+1)x+m=0有两个不等的实根,则m的取值范围是:
A.(-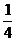 , +
, +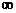 );B.(-
);B.(-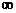 ,-
,-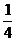 );C.[-
);C.[-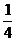 ,+
,+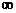 ];D.(-
];D.(-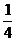 ,0)∪(0,+
,0)∪(0,+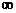 ).
).
提示:由m 0且
0且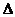 >0,得m<-
>0,得m<-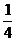 ,∴选D.
,∴选D.
例1 当m取什么实数时,方程4x2+(m-2)x+(m-5)=0分别有:
①两个实根; ②一正根和一负根;
③正根绝对值大于负根绝对值;④两根都大于1.
解 :设方程4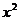 +(m-2)x+(m-5)=0的两根为
+(m-2)x+(m-5)=0的两根为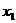 、
、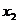
①若方程4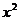 +(m-2)x+(m-5)=0有两个正根,则需满足:
+(m-2)x+(m-5)=0有两个正根,则需满足:

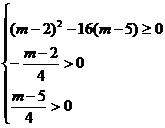
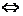
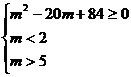
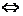
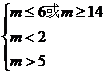
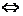 m∈φ.
m∈φ.
∴此时m的取值范围是φ,即原方程不可能有两个正根.
②若方程4 +(m-2)x+(m-5)=0有一正根和一负根,则需满足:
+(m-2)x+(m-5)=0有一正根和一负根,则需满足:
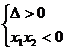
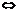
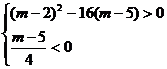
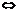 m<5.
m<5.
∴此时m的取值范围是(-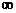 ,5).
,5).
③若方程4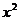 +(m-2)x+(m-5)=0的正根绝对值大于负根绝对值,则需满足:
+(m-2)x+(m-5)=0的正根绝对值大于负根绝对值,则需满足:
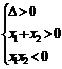
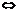 m<2.
m<2.
∴此时m的取值范围是(-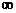 ,2).
,2).
④错解:若方程4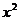 +(m-2)x+(m-5)=0的两根都大于1,则需满足:
+(m-2)x+(m-5)=0的两根都大于1,则需满足:
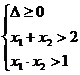
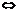
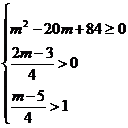
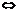 m∈(
m∈(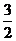 ,6)
,6)
∴此时m的取值范围是(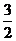 ,6),即原方程不可能两根都大于1.
,6),即原方程不可能两根都大于1.
正解:若方程4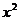 +(m-2)x+(m-5)=0的两根都大于1,则需满足:
+(m-2)x+(m-5)=0的两根都大于1,则需满足:
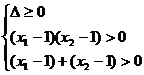
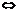
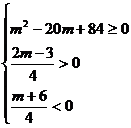
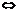 m∈φ.
m∈φ.
∴此时m的取值范围是φ,即原方程不可能两根都大于1.
说明:解这类题要充分利用判别式和韦达定理.
例2.已知方程2(k+1)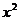 +4kx+3k-2=0有两个负实根,求实数k的取值范围.
+4kx+3k-2=0有两个负实根,求实数k的取值范围.
解:要原方程有两个负实根,必须:
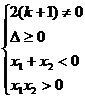
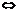
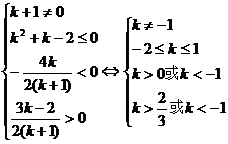 .
.
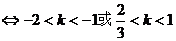
∴实数k的取值范围是{k|-2<k<-1或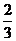 <k<1}.
<k<1}.
韦达定理:
方程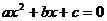 (
(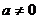 )的二实根为
)的二实根为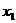 、
、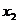 ,则
,则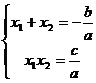
21.(本小题满分13分)
已知函数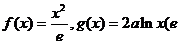 为自然对数的底数)
为自然对数的底数)
(1)求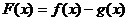 的单调区间,若
的单调区间,若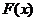 有最值,请求出最值;
有最值,请求出最值;
(2)是否存在正常数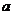 ,使
,使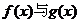 的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出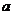 的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
21.(本小题满分13分)
已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为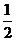 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;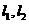 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,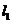 交E于A,B两点,
交E于A,B两点,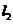 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。
(1)求椭圆E的方程;
(2)求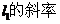 k的取值范围;
k的取值范围;
(3)求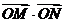 的取值范围。
的取值范围。
19.(本小题满分13分)
在数列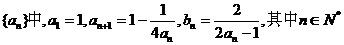 。
。
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列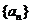 的通项公式
的通项公式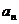 ;
;
(2)设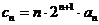 ,求数列
,求数列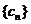 的前
的前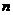 项和。
项和。
18.(本小题满分12分)
在如图所示的空间几何体中,平面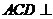 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在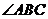 的平分线上。
的平分线上。
(1)求证:DE//平面ABC;
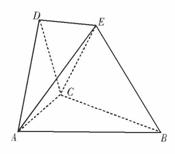 (2)求二面角E-BC-A的余弦;
(2)求二面角E-BC-A的余弦;
(3)求多面体ABCDE的体积。
17.(本小题满分12分)
甲乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码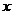 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码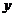 ,设随机变量
,设随机变量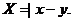
(1)求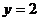 的概率;
的概率;
(2)求随机变量X的分布列及数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com