
3、醇的同分异构体
思考:写出C4H10O的同分异构体。
2、醇的命名
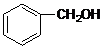
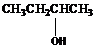
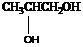
1、 醇的分类
一元醇:
醇的分类
一元醇:
 按羟基数目分 二元醇:
按羟基数目分 二元醇:
多元醇:
 醇
饱和脂肪醇:
醇
饱和脂肪醇:
 脂肪醇
脂肪醇
按烃基的类别分 不饱和脂肪醇:
芳香醇:
15.(2008·江西)等差数列{an}各项均为正整数,a1=3,前n项和为Sn,等比数列{bn}中,b1=1,且b2S2=64,{ban}是公比为64的等比数列.
(1)求an与bn;
(2)证明:++…+<.
(1)解:设{an}的公差为d,{bn}的公比为q,则d为正整数,
an=3+(n-1)d,bn=qn-1.
依题意有①
由(6+d)q=64知q为正有理数,又由q=2知,d为6的因子1,2,3,6之一,解①得d=2,q=8.
故an=3+2(n-1)=2n+1,bn=8n-1.
(2)证明:Sn=3+5+…+(2n+1)=n(n+2),
所以++…+=+++…+=
=<.
14.在等差数列{an}中,已知a1=20,前n项和为Sn,且S10=S15,求当n取何值时,Sn取得最大值,并求出它的最大值.
分析:(1)由a1=20及S10=S15可求得d,进而求得通项,由通项得到此数列前多少项为正,或利用Sn是关于n的二次函数,利用二次函数求最值的方法求解.(2)利用等差数列的性质,判断出数列从第几项开始变号.
解法一:∵a1=20,S10=S15,
∴10×20+d=15×20+d,
∴d=-.
∴an=20+(n-1)×(-)=-n+.
∴a13=0.
即当n≤12时,an>0,n≥14时,an<0.
∴当n=12或13时,Sn取得最大值,且最大值为
S12=S13=12×20+×(-)=130.
解法二:同解法一求得d=-.
∴Sn=20n+·(-)
=-n2+n
=-(n-)2+.
∵n∈N+,∴当n=12或13时,Sn有最大值,
且最大值为S12=S13=130.
解法三:同解法一得d=-.
又由S10=S15,得a11+a12+a13+a14+a15=0.
∴5a13=0,即a13=0.
∴当n=12或13时,Sn有最大值,
且最大值为S12=S13=130.
13.已知数列{an}中,a1=,an=2-(n≥2,n∈N*),数列{bn}满足bn=(n∈N*).
(1)求证:数列{bn}是等差数列;
(2)求数列{an}中的最大项和最小项,并说明理由.
(1)证明:因为an=2-(n≥2,n∈N*),bn=.
所以当n≥2时,bn-bn-1=-
=-=-=1.
又b1==-.
所以,数列{bn}是以-为首项,以1为公差的等差数列.
(2)解:由(1)知,bn=n-,
则an=1+=1+.
设函数f(x)=1+,易知f(x)在区间(-∞,)和(,+∞)内为减函数.
所以,当n=3时,an取得最小值-1;
当n=4时,an取得最大值3.
12.等差数列{an}的奇数项的和为216,偶数项的和为192,首项为1,项数为奇数,求此数列的末项和通项公式.
解:设等差数列{an}的项数为2m+1,公差为d,
则数列的中间项为am+1,奇数项有m+1项,偶数项有m项.
依题意,有
S奇=(m+1)am+1=216①
S偶=mam+1=192②
①÷②,得=,解得,m=8,
∴数列共有2m+1=17项,把m=8代入②,得a9=24,
又∵a1+a17=2a9,
∴a17=2a9-a1=47,且d==.
an=1+(n-1)×=(n∈N*,n≤17).
11.(2008·四川非延考区)设等差数列{an}的前n项和为Sn,若S4≥10,S5≤15,则a4的最大值为________.
答案:4
解法一:a5=S5-S4≤5,
S5=a1+a2+…+a5=5a3≤15,
a3≤3,则a4=≤4,a4的最大值为4,故填4.
解法二:
⇒a4≤4.
故a4的最大值为4.
解法三:本题也可利用线性规划知识求解.
由题意得:
⇒a4=a1+3d.
画出可行域求目标函数a4=a1+3d的最大值即当直线a4=a1+3d过可行域内(1,1)点时截距最大,此时a4=4.
10.(2008·重庆)设Sn是等差数列{an}的前n项和,a12=-8,S9=-9,则S16=________.
答案:-72
解析:S9=9a5=-9,
∴a5=-1,S16=8(a5+a12)=-72.
9.(2009·北京宣武4月)在等差数列{an}中,已知a1+2a8+a15=96,则2a9-a10=________.
答案:24
解析:等差数列{an},由a1+2a8+a15=96得4a8=96,a8=24,则2a9-a10=a9+a9-a10=a9-d=a8=24,故填24.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com