
3.求下列直线的斜率和在 轴上的截距,并画出图形:
轴上的截距,并画出图形:
(1)3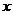 +
+ -5=0;(2)
-5=0;(2)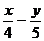 =1;(3)
=1;(3) 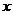 +2
+2 =0;
=0;
(4)7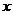 -6
-6 +4=0;(5)2
+4=0;(5)2 -7=0.
-7=0.
解:(1)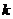 =-3,在
=-3,在 轴上截距为5
轴上截距为5
(2)化成斜截式得 =
=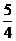
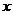 -5∴
-5∴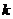 =
=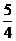 ,b=-5.
,b=-5.
(3)化成斜截式得 =-
=-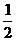
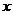 ∴
∴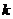 =-
=-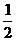 ,b=0.
,b=0.
(4)化成斜截式得 =
=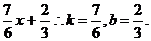
(5)化成斜截式得 =
= ,∴
,∴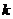 =0,b=
=0,b= .
.
图形(略)
2.已知直线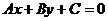
(1)当B≠0时,斜率是多少?当B=0时呢?
(2)系数取什么值时,方程表示通过原点的直线?
答:(1)当B≠0时,方程可化为斜截式: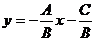 ∴斜率
∴斜率 .
.
当B=0时,A≠0时,方程化为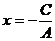 与
与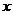 轴垂直,所以斜率不存在.
轴垂直,所以斜率不存在.
(2)若方程表示通过原点的直线,则(0,0)符合直线方程,则C=0.
所以C=0时,方程表示通过原点的直线.
课本P43练习
1.根据下列各条件写出直线的方程,并且化成一般式:
(1)斜率是-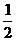 ,经过点A(8,-2);
,经过点A(8,-2);
(2)经过点B(4,2),平行于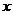 轴;
轴;
(3)在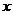 轴和
轴和 轴上的截距分别是
轴上的截距分别是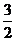 ,-3;
,-3;
(4)经过两点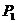 (3,-2)、
(3,-2)、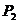 (5,-4).
(5,-4).
解:(1)由点斜式得 -(-2)=-
-(-2)=-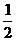 (
(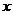 -8)
-8)
化成一般式得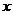 +2
+2 -4=0
-4=0
(2)由斜截式得 =2,化成一般式得
=2,化成一般式得 -2=0
-2=0
(3)由截距式得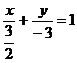 ,化成一般式得2
,化成一般式得2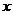 -
- -3=0
-3=0
(4)由两点式得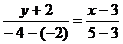 ,化成一般式得
,化成一般式得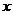 +
+ -1=0
-1=0
例1 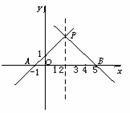 (2001年全国)设A、B是
(2001年全国)设A、B是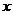 轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为
轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为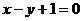 ,则直线PB的方程是
,则直线PB的方程是
A.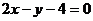 B.
B. 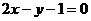 2
2
C.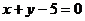 D.
D.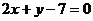
解法一:由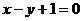 得A(-1,0).
得A(-1,0).
又|PA|=|PB|知点P为AB中垂线上的点,故B(5,0),且所求直线的倾斜角与已知直线倾斜角互补,则斜率互为相反数,故所求直线的斜率为-1,所以选C.
解法二: =0代入
=0代入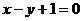 得A(-1,0).
得A(-1,0).
由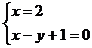 解得P(2,3).
解得P(2,3).
设B(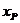 ,0),由|PA|=|PB|解得
,0),由|PA|=|PB|解得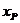 =5.
=5.
由两点式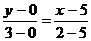
整理得PB直线方程: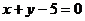 ,故选C
,故选C 
例2
(1997年全国)已知过原点O的一条直线与函数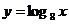 的图像交于A、B两点,分别过点A、B作
的图像交于A、B两点,分别过点A、B作 轴的平行线与函数的
轴的平行线与函数的 的图像交于C、D两点.
的图像交于C、D两点.
(Ⅰ)证明点C、D和原点O在同一条直线上;
(Ⅱ)当BC平行于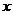 轴时,求点A的坐标.
轴时,求点A的坐标.
解:(Ⅰ)设点A、B的横坐标分别为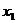 、
、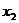 由题设知,
由题设知,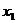 >1,
>1,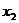 >1.则点A、B纵坐标分别为
>1.则点A、B纵坐标分别为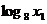 、
、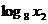 .
.
因为A、B在过点O的直线上,所以,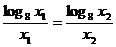
点C、D坐标分别为(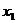 ,
,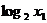 ),(
),(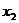 ,
,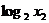 ).
).
由于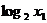 =
=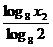 -3
-3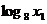 ,
,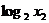 =
=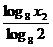 =3
=3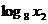
OC的斜率 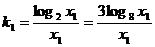 ,
,
OD的斜率 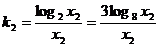 .
.
由此可知,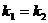 ,即O、C、D在同一条直线上.
,即O、C、D在同一条直线上.
 (Ⅱ)由于BC平行于x轴知
(Ⅱ)由于BC平行于x轴知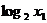 =
= 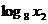 ,
,
即得 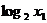 =
=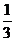
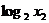 ,∴
,∴ 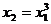 .
.
代入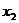
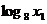 =
=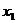
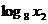
得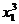
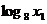 =3
=3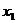
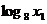 .
.
由于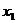 >1知
>1知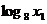 ≠0,∴
≠0,∴ 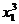 =3
=3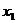 .
.
考虑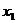 >1解得
>1解得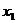 =
=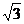 .于是点A的坐标为(
.于是点A的坐标为(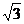 ,
, 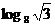 )
) 
5. 直线方程的一般形式:
点斜式、斜截式、两点式、截距式四种直线方程均可化成
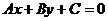 (其中A、B、C是常数,A、B不全为0)的形式,叫做直线方程的一般式
(其中A、B、C是常数,A、B不全为0)的形式,叫做直线方程的一般式
探究1:方程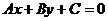 总表示直线吗?
总表示直线吗?
根据斜率存在不存在的分类标准,即B等于不等于0来进行分类讨论:
若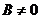 方程可化为
方程可化为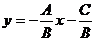 ,它是直线方程的斜截式,表示斜率为
,它是直线方程的斜截式,表示斜率为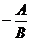 ,截距为
,截距为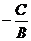 的直线;
的直线;
若B=0,方程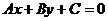 变成
变成 .由于A、B不全为0,所以
.由于A、B不全为0,所以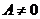 ,则方程变为
,则方程变为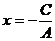 ,表示垂直于X轴的直线,即斜率不存在的直线.
,表示垂直于X轴的直线,即斜率不存在的直线.
结论:当A、B不全为0时,方程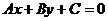 表示直线,并且它可以表示平面内的任何一条直线.
表示直线,并且它可以表示平面内的任何一条直线.
探究2:在平面直角坐标系中,任何直线的方程都可以表示成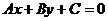 (A、B不全为0)的形式吗?
(A、B不全为0)的形式吗?
可采用多媒体动画演示,产生直线与 轴的不同位置关系(旋转),从而直观、形象地揭示分类讨论的本质,得出“任何一条直线的方程都是关于
轴的不同位置关系(旋转),从而直观、形象地揭示分类讨论的本质,得出“任何一条直线的方程都是关于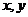 的二元一次方程,任何关于
的二元一次方程,任何关于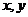 的二元一次方程都表示一条直线”的结论
的二元一次方程都表示一条直线”的结论
4.直线方程的截距式
定义:直线与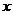 轴交于一点(
轴交于一点(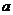 ,0)定义
,0)定义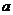 为直线在
为直线在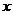 轴上的截距;直线与y轴交于一点(0,
轴上的截距;直线与y轴交于一点(0,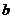 )定义
)定义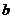 为直线在
为直线在 轴上的截距.
轴上的截距.
过A(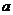 ,0) B(0,
,0) B(0, 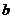 ) (
) (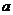 ,
,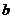 均不为0)的直线方程
均不为0)的直线方程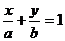 叫做直线方程的截距式.
叫做直线方程的截距式. 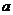 ,
,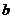 表示截距,它们可以是正,也可以是负,也可以为0.当截距为零时,不能用截距式.
表示截距,它们可以是正,也可以是负,也可以为0.当截距为零时,不能用截距式.
|
直线名称 |
已知条件 |
直线方程 |
使用范围 |
示意图 |
|
点斜式 |
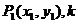 |
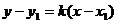 |
 |
|
|
斜截式 |
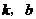 |
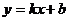 |
 |
|
|
两点式 |
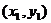 ( (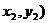 |
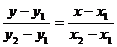 |
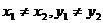 |
|
|
截距式 |
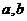 |
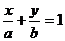 |
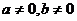 |
|
问题1:平面内的任一条直线,一定可以用以上四种形式之一来表示吗?
答:直线方程的四种特殊形式各自都有自己的优点,但都有局限性,即无法表示平面内的任一条直线.
问题2:是否存在某种形式的直线方程,它能表示平面内的任何一条直线?
3. 直线方程的两点式
当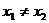 ,
,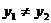 时,经过
时,经过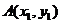 B(
B(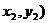 的直线的两点式方程可以写成:
的直线的两点式方程可以写成: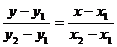 .
.
倾斜角是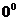 或
或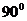 的直线不能用两点式公式表示.若要包含倾斜角为
的直线不能用两点式公式表示.若要包含倾斜角为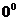 或
或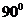 的直线,两点式应变为
的直线,两点式应变为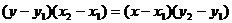 的形式.
的形式.
2.直线的斜截式方程-已知直线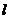 经过点P(0,b),并且它的斜率为k,直线
经过点P(0,b),并且它的斜率为k,直线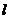 的方程:
的方程: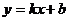 为斜截式.
为斜截式.
⑴斜截式是点斜式的特殊情况,某些情况下用斜截式比用点斜式更方便.
⑵斜截式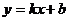 在形式上与一次函数的表达式一样,它们之间只有当
在形式上与一次函数的表达式一样,它们之间只有当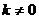 时,斜截式方程才是一次函数的表达式.
时,斜截式方程才是一次函数的表达式.
⑶斜截式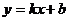 中,
中,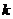 ,
,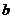 的几何意义
的几何意义
1. 直线的点斜式方程--已知直线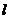 经过点
经过点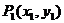 ,且斜率为
,且斜率为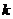 ,直线的方程:
,直线的方程: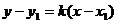 为直线方程的点斜式.
为直线方程的点斜式.
直线的斜率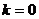 时,直线方程为
时,直线方程为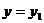 ;当直线的斜率
;当直线的斜率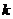 不存在时,不能用点斜式求它的方程,这时的直线方程为
不存在时,不能用点斜式求它的方程,这时的直线方程为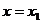 .
.
43.材料一: 我国02-08年CPI走势图
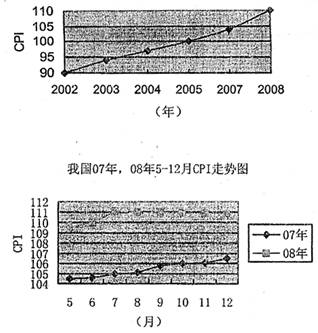
注:CPI(即居民消费物价指数),国际上反映居民家庭所购买的消费商品和服务价格水平变动情况的指标,并用它来反映通货膨胀程度。上述两张图表,以2005年CPI指数为100(%)
材料二:我国2008年12月的CPI比11月回落1.2%,2009年1、2月份,居民作废价格总水平同比继续下降,预计今年一季度CPI将同比去年第四季度下降1.0%。2008年12月8日至10日在北京举行的中央经济工作会议指出,在国际金融危机肆虐和国内经济增速下滑的大背景下,“保增长、促发展”成为2009年中央经济工作会议的主题。
(1)材料一的二张图表分别反映了哪些经济信息?(5分)
(2)针对去年前三季度较高的通货膨胀压力,我国政府采取哪些经济手段进行干预和调节。(2分)
(3)去年第四季度以来CPI同比下降和国内经济增速下滑,可能对今后一段时期经济运行和人民生活产生怎样的不利影响?(6分)
(4)你认为国家可以采取什么具体的财政政策措施来控制CPI指数的进一步走低?(2分,两条以上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com