练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在直角坐标平面中，若F1、F2为定点，P为动点，a＞0为常数，则“|PF1|+|PF2|=2a”是“点P的轨迹是以F1、F2为焦点，以2a为长轴的椭圆”的（　　）
    A．充要条件B．仅必要条件
    C．仅充分条件D．非充分且非必要条件
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    在直角坐标平面中，若F1、F2为定点，P为动点，a>0为常数，则“|PF1|+|PF2|=2a”是“点P的轨迹是以F1、F2为焦点，以2a为长轴的椭圆”的                      (   )

    A.充要条件  B.仅必要条件  C.仅充分条件 D.非充分且非必要条件

    查看答案和解析>>

    科目：高中数学 来源：金山区一模 题型：单选题

    在直角坐标平面中，若F1、F2为定点，P为动点，a＞0为常数，则“|PF1|+|PF2|=2a”是“点P的轨迹是以F1、F2为焦点，以2a为长轴的椭圆”的（　　）
    A．充要条件B．仅必要条件
    C．仅充分条件D．非充分且非必要条件

    查看答案和解析>>

    科目：高中数学 来源：2006年上海市金山区高考数学一模试卷（解析版） 题型：选择题

    在直角坐标平面中，若F1、F2为定点，P为动点，a＞0为常数，则“|PF1|+|PF2|=2a”是“点P的轨迹是以F1、F2为焦点，以2a为长轴的椭圆”的（ ）
    A．充要条件
    B．仅必要条件
    C．仅充分条件
    D．非充分且非必要条件

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在直角坐标平面中，若F1、F2为定点，P为动点，a>0为常数，则“|PF1|+|PF2|=2a”是“点P的轨迹是以F1、F2为焦点，以2a为长轴的椭圆”的                      (   )
    A.充要条件  B.仅必要条件  C.仅充分条件 D.非充分且非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在直角坐标平面中，若F1、F2为定点，P为动点，a＞0为常数，则“|PF1|+|PF2|=2a”是“点P的轨迹是以F1、F2为焦点，以2a为长轴的椭圆”的


    1. A.
      充要条件
    2. B.
      仅必要条件
    3. C.
      仅充分条件
    4. D.
      非充分且非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2005•金山区一模）在直角坐标平面中，若F1、F2为定点，P为动点，a＞0为常数，则“|PF1|+|PF2|=2a”是“点P的轨迹是以F1、F2为焦点，以2a为长轴的椭圆”的（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    平面直角坐标系xOy中，已知⊙M经过点F1（0，-c），F2（0，c），A（
    		3
    c，0）三点，其中c＞0．
    （1）求⊙M的标准方程（用含c的式子表示）；
    （2）已知椭圆
    y2
    a2
    +
    x2
    b2
    =1(a＞b＞0)    （其中a2-b2=c2）的左、右顶点分别为D、B，⊙M与x轴的两个交点分别为A、C，且A点在B点右侧，C点在D点右侧．
    ①求椭圆离心率的取值范围；
    ②若A、B、M、O、C、D（O为坐标原点）依次均匀分布在x轴上，问直线MF1与直线DF2的交点是否在一条定直线上？若是，请求出这条定直线的方程；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：南通模拟 题型：解答题

    平面直角坐标系xOy中，已知⊙M经过点F1（0，-c），F2（0，c），A（
    		3
    c，0）三点，其中c＞0．
    （1）求⊙M的标准方程（用含c的式子表示）；
    （2）已知椭圆
    y2
    a2
    +
    x2
    b2
    =1(a＞b＞0)    （其中a2-b2=c2）的左、右顶点分别为D、B，⊙M与x轴的两个交点分别为A、C，且A点在B点右侧，C点在D点右侧．
    ①求椭圆离心率的取值范围；
    ②若A、B、M、O、C、D（O为坐标原点）依次均匀分布在x轴上，问直线MF1与直线DF2的交点是否在一条定直线上？若是，请求出这条定直线的方程；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：浙江省模拟题 题型：解答题

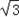    平面直角坐标系xOy中，已知⊙M经过点F1（0，﹣c），F2（0，c），A（c，0）三点，其中c＞0．
    （1）求⊙M的标准方程（用含c的式子表示）；
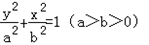    （2）已知椭圆（其中a2﹣b2=c2）的左、右顶点分别为D、B，⊙M与x轴的两个交点分别为A、C，且A点在B点右侧，C点在D点右侧．
    ①求椭圆离心率的取值范围；
    ②若A、B、M、O、C、D（O为坐标原点）依次均匀分布在x轴上，问直线MF1与直线DF2 的交点是否在一条定直线上？若是，请求出这条定直线的方程；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2013年宁夏吴忠市回民中学高考数学五模试卷（文科）（解析版） 题型：解答题

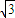    平面直角坐标系xOy中，已知⊙M经过点F1（0，-c），F2（0，c），A（c，0）三点，其中c＞0．
    （1）求⊙M的标准方程（用含c的式子表示）；
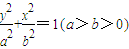    （2）已知椭圆（其中a2-b2=c2）的左、右顶点分别为D、B，⊙M与x轴的两个交点分别为A、C，且A点在B点右侧，C点在D点右侧．
    ①求椭圆离心率的取值范围；
    ②若A、B、M、O、C、D（O为坐标原点）依次均匀分布在x轴上，问直线MF1与直线DF2的交点是否在一条定直线上？若是，请求出这条定直线的方程；若不是，请说明理由．

    查看答案和解析>>


    同步练习册答案