
����Ŀ����ͼ��������y=![]() x2��
x2��![]() x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
��1����AB��OC�ij���
��2����E�ӵ�A��������x�����B�˶�����E���A��B���غϣ�������E��ֱ��lƽ��BC����AC�ڵ�D����AE�ij�Ϊm����ADE�����Ϊs����s����m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3���ڣ�2���������£�����CE������CDE��������ֵ����ʱ������Ե�EΪԲ�ģ���BC���е�Բ��������������������

���𰸡���1��AB=9��OC=9����2��s=![]() m2��0��m��9������3��
m2��0��m��9������3��![]() .
.
�������������������1����֪�����ߵĽ���ʽ����![]() ��ȷ��
��ȷ��![]() �����ꣻ��
�����ꣻ��![]() ʱ����ȷ��
ʱ����ȷ��![]() ������꣬����ȷ��
������꣬����ȷ��![]() �ij���
�ij���
��2��ֱ��![]() �ɵó�
�ɵó�![]() ���ƣ����ǵ�����ȵ������Ʊȵ�ƽ�����ɴ˵õ�����
���ƣ����ǵ�����ȵ������Ʊȵ�ƽ�����ɴ˵õ�����![]() �ĺ�����ϵʽ�����������������
�ĺ�����ϵʽ�����������������![]() ���
���![]() ���غϣ���ȷ��
���غϣ���ȷ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����������![]() �г�
�г�![]() ���������ʽ��
���������ʽ�� ![]() ������Ϊ
������Ϊ![]() ��������ɴ˿ɵù���
��������ɴ˿ɵù���![]() �ĺ�����ϵʽ�����ݺ��������ʿɵõ�
�ĺ�����ϵʽ�����ݺ��������ʿɵõ�![]() ���������Լ���ʱ
���������Լ���ʱ![]() ��ֵ��
��ֵ��
�ڹ�![]() ��
��![]() �Ĵ���
�Ĵ���![]() ��������߶εij���Ϊ��
��������߶εij���Ϊ��![]() ���е�
���е�![]() �İ뾶���ɸ�������������
�İ뾶���ɸ�������������![]() �õ�����ر����߶���øð뾶��ֵ���ɴ˵ý⣮
�õ�����ر����߶���øð뾶��ֵ���ɴ˵ý⣮
���������(1)��֪��������![]()
��x=0ʱ,y=9,��C(0,9)��
��y=0ʱ, ![]() ,����
,���� ![]() ,��A(3,0)��B(6,0)��
,��A(3,0)��B(6,0)��
��AB=9��OC=9.
(2) ![]()
����AED����ABC��
 ����
����  �ã�
�ã� ![]()

(3)�ⷨһ�� ![]()
![]()
��0<m<9��
�൱![]() ʱ,
ʱ, ![]() ȡ�����ֵ,���ֵΪ
ȡ�����ֵ,���ֵΪ![]() ��ʱ,
��ʱ, ![]()
��E��BC�����ڵ�M������EM����EM��BC����E�İ뾶Ϊr.
��![]() ��,
��, ![]()
![]()
����BOC����BME��
![]()
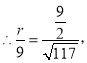
![]()
������![]() �������
������� 


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��ѡ��ѧ���μӡ�������д���������Ծ��꼶һ�ࡢ�����10��ѧ�����к�����д���ԣ��Ʒֲ���10���ƣ��÷־�ȡ���������ɼ��ﵽ6�ֻ�6������Ϊ���õ�9��Ϊ���㣬�ɼ����1��ʾ���������˳ɼ�����������2����
��1
һ�� | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
���� | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
��2
�༶ | ƽ���� | ��λ�� | ���� | ���� | ������ | ������ |
һ�� | 7.6 | 8 | 3.82 | 70% | 30% | |
���� | b | 7.5 | 10 | 4.94 | 80% | 40% |
��1���ڱ�2�У�a=�� ����b=�� ����
��2������˵����ļ����ʡ������ʾ�����һ�࣬���Զ����һ��ã���Ҳ������Ϊһ��ɼ��ȶ���ã�����������һ��ɼ��õ��������ɣ�
��3��һ�ࡢ��������ֵ���ͬѧ�Ա�ֱ���1��1Ů��2��1Ů���ִ�����������ֵ�ͬѧ�и���1��ͬѧ�μӡ�������д������������״ͼ���б������ǡ�ó鵽1��1Ů��λͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
1��2=![]() ����1��2��3��0��1��2��
����1��2��3��0��1��2��
2��3=![]() ����2��3��4��1��2��3��
����2��3��4��1��2��3��
3��4=![]() ����3��4��5��2��3��4��
����3��4��5��2��3��4��
��
���㣺3��[1��2+2��3+3��4+��+n��n+1��]=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������Ϊ�˽ⱾУ���꼶ѧ����1������������Ŀ��ѵ������������ȡ���꼶n��ѧ��������һ�β��ԣ��������Գɼ��ֳ����ࣺ���㡢���á������������ͳ�ƣ�����ͳ�ƽ�����Ƴ�����������������ͳ��ͼ.
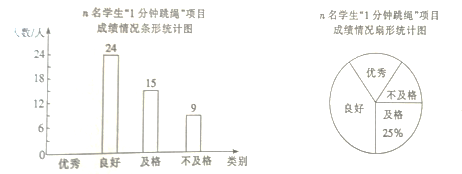
�����ͼ����Ϣ������������⣺
��1����n��ֵ.
��2��������ͳ��ͼ��������.
��3�����Ƹ�У���꼶800��ѧ���С�1������������Ŀ�ɼ�Ϊ�������ѧ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ʾ������
��ʾ������![]() ��������������磺
��������������磺![]() ��
��![]() ��
��![]() ����
����![]() ��ʾ����
��ʾ����![]() ����С���������磺
����С���������磺![]() ��
��![]() ��
��![]() .����������⣺
.����������⣺
��1��![]() = ,��
= ,��![]() = ��
= ��
��2����![]() =2����
=2����![]() ��ȡֵ��Χ�� ����
��ȡֵ��Χ�� ����![]() =��1����
=��1����![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
��3����֪![]() ��
��![]() ���㷽����
���㷽����![]() ����
����![]() ��
��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����о��С���ʮ�߽���Сѧ���鷨��������Ʒ��������֪ÿ��������Ʒ�ɼ���Ϊ![]() ����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
������ | Ƶ�� | �ٷֱ� |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
�ϼ� | ________ | 1 |

����������Ϣ������������⣺
��1������鷨��Ʒ�����ɼ��ĵ����Dz���_____����ղ顱�������顱����������_____��
��2������ϱ�������ȫ�鷨��Ʒ�����ɼ�Ƶ��ֱ��ͼ��
��3����80�֣���80�֣����ϵ��鷨��Ʒ������Ϊ�ȼ������Թ���ȫ�л�õȼ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ�ƻ��������ɸ����ֹ�����������ֹ�������.�������![]() �����ֹ��������
�����ֹ��������![]() �����ֹ�������һ����Ҫ����
�����ֹ�������һ����Ҫ����![]() Ԫ;�������
Ԫ;�������![]() �����ֹ��������
�����ֹ��������![]() �����ֹ�������һ����Ҫ����
�����ֹ�������һ����Ҫ����![]() Ԫ.
Ԫ.
![]() ��ÿ�����ֹ��������ÿ�����ֹ�������ļ۸�ֱ��Ƕ���Ԫ?
��ÿ�����ֹ��������ÿ�����ֹ�������ļ۸�ֱ��Ƕ���Ԫ?
![]() ���ѧУҪ������ֹ�����������ֹ�������
���ѧУҪ������ֹ�����������ֹ�������![]() ��������Ԥ���ܷ��ò�����3080Ԫ����ô��ѧУ�����ܹ�����ٸ����ֹ�������
��������Ԥ���ܷ��ò�����3080Ԫ����ô��ѧУ�����ܹ�����ٸ����ֹ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ҫ������������˫���յ���������������������е��鷽ʽ��
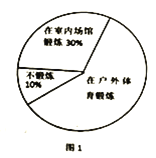
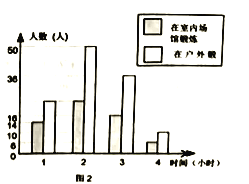
A.��һ���߲�סլ¥��ѡȡ200������
B.�Ӳ�ͬסլ¥�����ѡȡ200����
C.ѡȡ������200����Уѧ��
��1���������鷽ʽ���������___________________��
��2����������ĵ��鷽ʽ�õ��������Ƴ�����ͳ��ͼ����ͼ1����Ƶ���ֲ�ֱ��ͼ����ͼ2��.����������У�200������˫�����ڻ���������������_____________�ˣ�
��3�������е�200�������ڻ������1Сʱ������Ϊ__________________��
��4��������Ƹ�����1600������˫������������ʱ�䲻����3Сʱ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC=90����AB=6cm��AD=24cm��BC��CD�ij���֮��Ϊ34cm������C��ֱ��l�ϵ�һ�����㣬����̽����C���B�ж�Զʱ����ACD����DCΪб�ߵ�ֱ�������Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com