
(本题满分10分)如图,Rt△ABC在平面直角坐标系中,BC在X轴上,B(﹣1,0)、A(0,2),AC⊥AB.

(1)求线段OC的长.
(2)点P从B点出发以每秒4个单位的速度沿x轴正半轴运动,点Q从A点出发沿线段AC以 个单位每秒速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围.
个单位每秒速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围.
(3)Q点沿射线AC按原速度运动,⊙G过A、B、Q三点,是否有这样的t值使点P在⊙G上、如果有求t值,如果没有说明理由.
(1)4;(2) (3)
(3)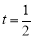 .
.
【解析】
试题分析:(1)利用△AOB∽△COA即可求得OC=4.
(2)分当P在BC上,Q在线段AC上时、当P在BC延长线上,Q在线段AC上时、当C、P、Q都在同一直线上利用△CQD∽△CAO求得t值即可.
(3)若点P在圆G上,因为AC⊥AB,所以BQ是直径,所以∠BPQ=Rt∠,即PQ⊥BC,则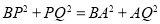 ,得到有关t的式子求解即可.
,得到有关t的式子求解即可.
试题解析:(1)∵AC⊥AB,∴∠ABO+∠ACO=90°,
∵∠BAO+∠ABO=90°,∴∠BAO=∠ACO,∠ABO=∠OAC,∴△AOB∽△COA,∴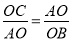 ,
,
∵B(﹣1,0)、A(0,2),∴OA=2,OB=1,∴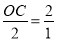 ,∴OC=4;
,∴OC=4;
(2)①当P在BC上,Q在线段AC上时,(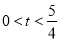 )过点Q作QD⊥BC于D,
)过点Q作QD⊥BC于D,
如图所示,则CQ=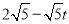 ,CP=5﹣4t,
,CP=5﹣4t,
由△CQD∽△CAO可得QD=2﹣t,所以S=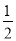 CP•QD=
CP•QD=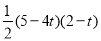 ,
,
即S=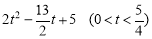 ;
;
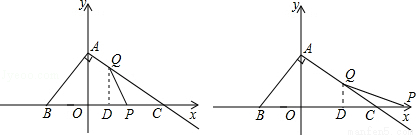
②当P在BC延长线上,Q在线段AC上时(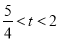 ),过点Q作QD⊥BC于D,
),过点Q作QD⊥BC于D,
如图所示,则CQ=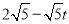 ,CP=4t﹣5,
,CP=4t﹣5,
由△CQD∽△CAO可得QD=2﹣t,所以S=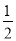 CP•QD=
CP•QD=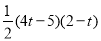 ,
,
即S=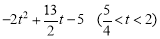 ,
,
③当t=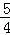 或t=2时C、P、Q都在同一直线上,S=0.
或t=2时C、P、Q都在同一直线上,S=0.
∴ ;
;
(3)若点P在圆G上,因为AC⊥AB,所以BQ是直径,所以∠BPQ=90°,即PQ⊥BC,
则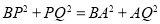 ,得:
,得: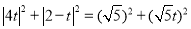 ,
,
解得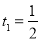 ,
,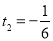 (不合题意,舍去),所以当
(不合题意,舍去),所以当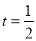 时,点P在圆G上.
时,点P在圆G上.
考点:1.相似三角形的判定与性质;2.坐标与图形性质;3.圆周角定理.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:2014-2015学年广东省云浮市郁南县三八年级上学期期中联考数学试卷(解析版) 题型:选择题
如图所示,在RtΔACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )

A. 9 B. 8 C. 7 D. 6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县片区三九年级上学期期中联考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点。
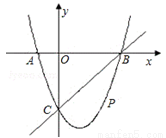
(1)求这个二次函数的表达式。
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC ∽△ADE的是( )
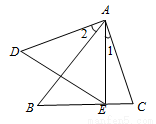
A.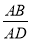 =
= 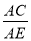 B.
B.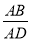 =
= 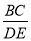 C.∠B=∠D D.∠C=∠AED
C.∠B=∠D D.∠C=∠AED
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D 为AC上一点,∠AOD=∠C.

(1)求证:OD⊥AC;
(2)若AE=8,cosA= ,求OD的长.
,求OD的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
△ABC是⊙O的内接三角形,若∠AOC =100°,则∠ABC的度数等于 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(7分)观察下列各式: ;
; ;
; ……,
……,
请你猜想:
 _______,
_______,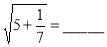 .
.
计算(请写出推导过程):
请你将猜想到的规律用含有自然数n(n≥1)的代数式表达出来:
_______________________________________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com