
��ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬A����ԭ�����࣬B�������Ϊ��3��0������y�ύ��C��0����3���㣬��P��ֱ��BC�·�����������һ���㡣
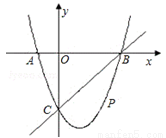
��1����������κ����ı���ʽ��
��2������PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɡ�
��3������P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC����������
��1��y=x2-2x-3.��2����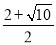 ��-
��-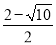 ����3��
����3��
��������
�����������1����B��C��������������ߵĽ���ʽ�м�����ô���ϵ����ֵ��
��2���������εĶԽ����ഹֱƽ�֣����ı���POP��CΪ���Σ���ôP�����OC�Ĵ�ֱƽ�����ϣ��ݴ˿����P��������꣬���������ߵĽ���ʽ�м������P������ꣻ
��3�����ڡ�ABC�����Ϊ��ֵ�����ı���ABPC��������ʱ����BPC��������P��y���ƽ���ߣ���ֱ��BC��Q����x����F�������ֱ��BC�Ľ���ʽ�������P��ĺ����꣬Ȼ����������ߺ�ֱ��BC�Ľ���ʽ���Q��P�������꣬���ɵõ�PQ�ij�����PQΪ�ף�B�������ľ���ֵΪ������á�BPC��������ɴ˿ɵõ������ı���ACPB�������P�������ĺ�����ϵʽ�����ݺ��������ʼ�������ı���ABPC������������Ӧ��P�����꣮
�����������1����B��C�������������
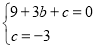 ��
��
��ã�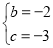 ��
��
���Զ��κ����ı���ʽΪ��y=x2-2x-3.
��2�����ڵ�P��ʹ�ı���POP��CΪ���Σ�
��P������Ϊ��x��x2-2x-3����PP�佻CO��E
���ı���POP��C�����Σ�����PC=PO��
����PP�䣬��PE��CO��E��
��C��0��-3����
��CO=3��
�֡�OE=EC��
��OE=EC=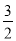
��y=-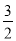 ��
��
��x2-2x-3=-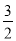
���x1=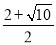 ��x2=
��x2=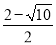 ���������⣬��ȥ����
���������⣬��ȥ����
��P���������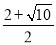 ��-
��-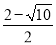 ��
��
��3������P��y���ƽ������BC���ڵ�Q����OB���ڵ�F����P��x��x2-2x-3����
��ֱ��BC�Ľ���ʽΪ��y=kx+d��
��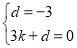 ��
��
��ã�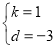
��ֱ��BC�Ľ���ʽΪy=x-3��
��Q���������x��x-3����
��0=x2-2x-3��
��ã�x1=-1��x2=3��
��AO=1��AB=4��
S�ı���ABPC=S��ABC+S��BPQ+S��CPQ
=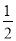 AB•OC+
AB•OC+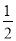 QP•BF+
QP•BF+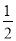 QP•OF
QP•OF
=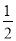 ��4��3+
��4��3+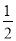 (-x2+3x)��3
(-x2+3x)��3
=-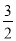 (x-
(x-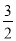 )2+
)2+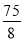
��x=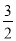 ʱ���ı���ABPC��������
ʱ���ı���ABPC��������
��ʱP�������Ϊ(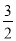 ��-
��-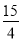 )���ı���ABPC����������ֵΪ
)���ı���ABPC����������ֵΪ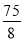 ��
��
���㣺���κ����ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ���꼶10���¿���ѧ�Ծ��������棩 ���ͣ������
��ͼ�еġ�ABC�����б任��������Ӧ��ͼ�Σ�ָ����������������������ı仯��
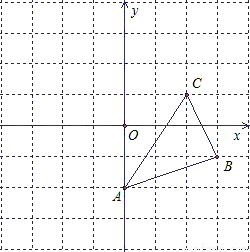
��1����y������ƽ��2����λ��
��2������y��Գ� ��
��3���ڸ����ķ���ͼ�У��Ե�BΪλ�����ģ��Ŵ�2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��㶫ʡ�Ƹ��������������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ������
һ���������,ÿ���ڽǶ����,����ÿ����ǵ������������ڽǵ� , ���������εı������ڽǺ�.
, ���������εı������ڽǺ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��㶫ʡ�Ƹ���������Ƭ�������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ������
�������� ����ƽ��2����λ�õ��������ߵĽ���ʽ��
����ƽ��2����λ�õ��������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��㶫ʡ�Ƹ���������Ƭ�������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ������
����һ�鳤20cm����10cm�ij�������Ƥ���������ĸ��Ƿֱ��ȥһ����С��ȫ��ͬ��С�����Σ���ʣ��IJ�������һ�������Ϊ56cm2���dz�������ӣ������ȥ��С�����εı߳���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������8�֣����壺��ͼ1����C���߶�AB�ϣ�������AC2=BC•AB����Ƶ�CΪ�߶�AB�Ļƽ�ָ�㣮��ͼ2����ABC�У�AB=AC=1����A=36�㣬BDƽ�֡�ABC��AC�ڵ�D��

��1����֤����D���߶�AC�Ļƽ�ָ�㣻
��2������߶�AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ھ���ABCD�У�AD=4��DC=3������ADC�Ƶ�A����ʱ�뷽����ת����AEF����A��B��Eͬһֱ���ϣ�����AC��ɨ�������Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������10�֣���ͼ��Rt��ABC��ƽ��ֱ������ϵ�У�BC��X���ϣ�B����1��0����A��0��2����AC��AB��

��1�����߶�OC�ij���
��2����P��B�������ÿ��4����λ���ٶ���x���������˶�����Q��A��������߶�AC�� ����λÿ���ٶ����C�� ������һ��ֹͣ�˶�����һ��Ҳ��ֹ֮ͣ�����CPQ���� ��ΪS������ͬʱ�˶����˶���ʱ��Ϊt�룬��S��t֮���ϵʽ����д���Ա���ȡֵ��Χ��
����λÿ���ٶ����C�� ������һ��ֹͣ�˶�����һ��Ҳ��ֹ֮ͣ�����CPQ���� ��ΪS������ͬʱ�˶����˶���ʱ��Ϊt�룬��S��t֮���ϵʽ����д���Ա���ȡֵ��Χ��
��3��Q��������AC��ԭ�ٶ��˶�����G��A��B��Q���㣬�Ƿ���������tֵʹ��P�ڡ�G�ϡ��������tֵ�����û��˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com