
【题目】如图,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B的左侧),直线
轴交于A,B两点(点A在点B的左侧),直线![]() 与抛物线交于
与抛物线交于![]() 两点,其中点
两点,其中点![]() 的横坐标为2.
的横坐标为2.
(1)求A,B两点的坐标及直线AC的表达式;
(2)P是线段AC上一动点(P与A,C不重合),过点P作![]() 轴的平行线交抛物线于点E,求
轴的平行线交抛物线于点E,求![]() 面积的最大值;
面积的最大值;
(3)点H是抛物线上一动点,在![]() 轴上是否存在点F,使得
轴上是否存在点F,使得![]() 四个点为顶点的四边形是平行四边形?如果存在请直接写出所有满足条件的点F坐标;如果不存在,请说明理由.
四个点为顶点的四边形是平行四边形?如果存在请直接写出所有满足条件的点F坐标;如果不存在,请说明理由.

【答案】(1)A(1,0),B(3,0),![]() ;(2)
;(2)![]() 面积的最大值为
面积的最大值为![]() ;(3)存在,
;(3)存在,![]() ,
,![]() .
.
【解析】
(1)令抛物线y=x2-2x-3=0,求出x的值,即可求A,B两点的坐标,根据两点式求出直线AC的函数表达式;
(2)设P点的横坐标为x(-1≤x≤2),求出P、E的坐标,用x表示出线段PE的长,求出PE的最大值,进而求出△ACE的面积最大值;
(3)结合图形,分两类进行讨论,①CF平行x轴,如图1,此时可以求出F点两个坐标;②CF不平行x轴,如题中的图2,此时可以求出F点的两个坐标.
(1)令y=0,解得x1=-1或x2=3,
∴A(-1,0),B(3,0);
将C点的横坐标x=2代入y=x2-2x-3得y=-3,
∴C(2,-3),
设直线AC的解析式为:y=kx+b,
把A(-1,0),C(2,-3)代入直线解析式得,
![]()
解得,![]()
∴直线AC的函数解析式是y=-x-1,
(2)设P点的横坐标为x(-1≤x≤2),
则P、E的坐标分别为:P(x,-x-1),E(x,x2-2x-3),
∵P点在E点的上方,PE=(-x-1)-(x2-2x-3)=-x2+x+2=-(x-![]() )2+
)2+![]() ,
,
∴当x=![]() 时,PE的最大值=
时,PE的最大值=![]() ,
,
△ACE的面积最大值=![]() PE[2-(-1)]=
PE[2-(-1)]= ![]() PE=
PE=![]() ,
,
(3)存在,如图1,若AF∥CH,此时的D和H点重合,CD=2,则AF=2,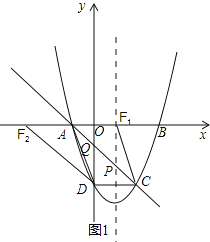
于是可得F1(1,0),F2(-3,0),
如图2,根据点A和F的坐标中点和点C和点H的坐标中点相同,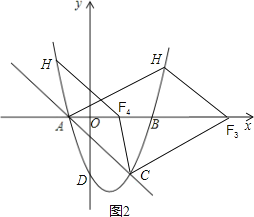
再根据![]()
求出![]()
综上所述满足条件的点F的坐标为![]() ,
,![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,点E在矩形ABCD的边AD上,AD=6,tan∠ACD=![]() ,连接CE,线段CE绕点C旋转90°,得到线段CF,以线段EF为直径做⊙O.
,连接CE,线段CE绕点C旋转90°,得到线段CF,以线段EF为直径做⊙O.
(1)请说明点C一定在⊙O上的理由;
(2)点M在⊙O上,如图2,MC为⊙O的直径,求证:点M到AD的距离等于线段DE的长;
(3)当△AEM面积取得最大值时,求⊙O半径的长;
(4)当⊙O与矩形ABCD的边相切时,计算扇形OCF的面积.
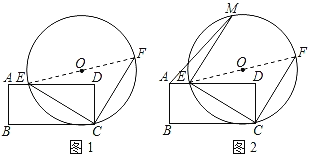
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BC的中点,连接DE,P是DE上一点,∠BPC=90°,延长CP交AD于点F.⊙O经过P、D、F,交CD于点G.
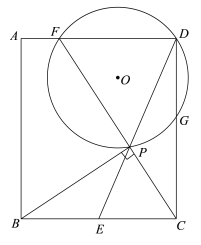
(1)求证:DF![]() DP;
DP;
(2)若![]() ,
,![]() ,求DG的长;
,求DG的长;
(3)连接BF,若BF是⊙O的切线,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
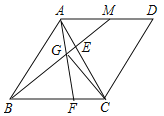
【题目】如图,在菱形ABCD中,∠ABC=60°,M为AD的中点,连接BM,交AC于E,在CB上取一点F,使得CF=AE,连接AF,交BM于G,连接CG.
(1)求∠BGF的度数;
(2)求![]() 的值;
的值;
(3)求证:BG⊥CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
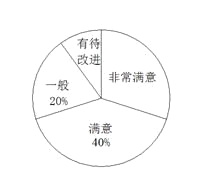
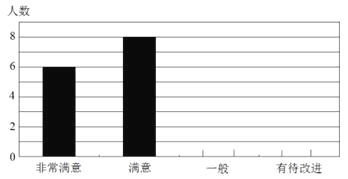
【题目】2012年4月5日下午,重庆一中初2013级“智力快车”比赛的决赛在渝北校区正式进行.“智力快车”活动是我校综合实践课程的传统版块,已有多年历史,比赛试题的内容涉及到文史艺哲科技等多个方面.随着时代的变化,其活动项目也在不断更新.今年的比赛除了继承传统的“快速判断”、“猜猜看”、“英语平台”、“风险提速”四个环节外,特新增了“动手动脑”一项.比赛结束后,一综合实践小组成员就新增环节的满意程度,对现场的观众进行了抽样调查,给予评分,其中:非常满意——5分,满意——4分,一般——3分,有待改进——2分,并将调查结果制作成了如下的两幅不完整的统计图:

![]()
(1)本次共调查了 名同学,本次调查同学评分的平均得分为 分;
(2)将条形统计图补充完整;
(3)如果评价为“一般”的只有一名是男生,评价为“有待改进”的只有一名是女生,
针对“动手动脑”环节的情况,综合实践小组的成员分别从评价为“一般”和评价
为“有待改进”的两组中,分别随机选出一名同学谈谈意见和建议,请你用列表或画树状图的方法求出所选两名同学刚好都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
已知:∠α,直线l和l上两点A,B.
求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
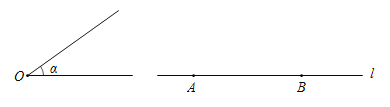
小刚的做法如下:
①以∠α的顶点O为圆心,任意长为半径作弧,交两边于M,N;以A为圆心,同样长为半径作弧,交直线l于点P;
②以P为圆心,MN的长为半径作弧,两弧交于点Q,作射线AQ;
③以B为圆心,任意长为半径作弧,交直线l于E,F;
④分别以E,F为圆心,大于![]() 长为半径作弧,两弧在直线l上方交于点G,作射线BG;
长为半径作弧,两弧在直线l上方交于点G,作射线BG;
⑤射线AQ与射线BG交于点C.Rt△ABC即为所求.
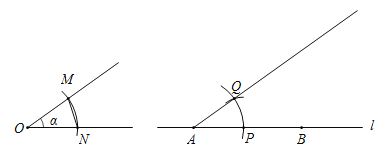
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
连接PQ
在△OMN和△AQP中,
∵ON=AP,PQ=NM,OM=AQ
∴△OMN ≌△AQP(__________)(填写推理依据)
∴∠PAQ=∠O=α
∵CE=CF,BE=BF
∴CB⊥EF(____________________________)(填写推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=30°,AB=AC,将线段AC绕点A逆时针旋转α°(0<α<180),得到线段AD,连接BD,交AC于点P.
(1)当α=90时,
①依题意补全图形;
②求证:PD=2PB;
(2)写出一个α的值,使得PD=![]() PB成立,并证明.
PB成立,并证明.
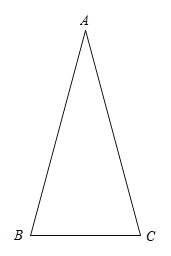
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 直径,作
直径,作![]() 的内接正六边形,甲、乙两人的作法分别如下:
的内接正六边形,甲、乙两人的作法分别如下:
甲:1.作![]() 的中垂线,交圆
的中垂线,交圆![]() 于
于![]() 两点;2.作
两点;2.作![]() 的中垂线,交圆
的中垂线,交圆![]() 于
于![]() 两点;3.顺次连接
两点;3.顺次连接![]() 六个点,六边形即为所求;
六个点,六边形即为所求;
乙:1.以![]() 为圆心,
为圆心,![]() 长为半径作弧,交圆
长为半径作弧,交圆![]() 于
于![]() 两点;2.以
两点;2.以![]() 为圆心,
为圆心,![]() 长为半径作弧,交圆
长为半径作弧,交圆![]() 于
于![]() 两点;3.顺次连接
两点;3.顺次连接![]() 六个点,六边形即为所求;
六个点,六边形即为所求;
对于甲、乙两人的作法,可判断( )
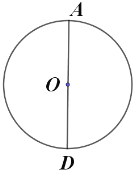
A.甲对,乙不对B.甲不对,乙对
C.两人都不对D.两人都对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com