
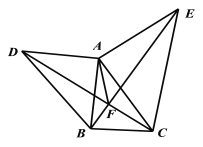
【题目】如图,在△ABC外分别以AB,AC为边作两个大小不同的等腰直角三角形ABD和等腰直角三角形ACE,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DCBE交于F点.
(1)请你找出一对全等的三角形,并加以证明;
(2)直线DC、BE是否互相垂直,请说明理由;
(3)求证:∠DFA=∠EFA.
科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表所示:
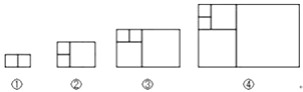

若按此规律继续作长方形,则序号为⑧的长方形周长是( )
A. 288 B. 178 C. 28 D. 110
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF. 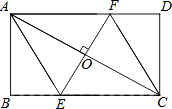
(1)求证:四边形AECF是菱形;
(2)若AB= ![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 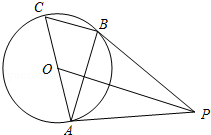
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
人数 | 52 | 60 | 62 | 54 | 58 | 62 |
A.平均数是58
B.中位数是58
C.极差是40
D.众数是60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 三个顶点的坐标分别为 A(1,1),B(4,2),C(3,4).
(1)请画出△ABC 向左平移 5 个单位长度后得到的△A1B1C1;
(2)在 x 轴上求作一点 P,使△PAB 的周长最小,请画出△PAB,并直接写出 P 的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com