
【题目】已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.

【答案】(1)证明见解析;(2)(1)中的结论还成立,证明见解析;(3)四边形![]() 的面积为
的面积为![]() .
.
【解析】
(1)根据菱形的性质及已知,得到![]() ,再证
,再证![]() ,
,
根据三角形全等的性质即可得到结论;
(2)作![]() ,垂足分别为点
,垂足分别为点![]() ,证明
,证明![]() ,根据三角形全等的性质即可得到结论;
,根据三角形全等的性质即可得到结论;
(3)根据菱形的面积公式,结合(2)的结论解答.
解:(1)∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
在![]() 和
和![]() 中,
中,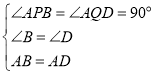 ,
,
∴![]() ,
,
∴![]() .
.
(2)若![]() 与
与![]() 不垂直,(1)中的结论还成立证明如下:
不垂直,(1)中的结论还成立证明如下:
如图,作![]() ,垂足分别为点
,垂足分别为点![]() .
.
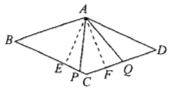
由(1)可得![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,∴
,∴![]() .
.
(3)如图,连接![]() 交于点
交于点![]() .
.

∵![]() ,∴
,∴![]() 为等边三角形,
为等边三角形,
∵![]() ,∴
,∴![]() ,同理,
,同理,![]() ,
,
∴四边形![]() 的面积
的面积![]() 四边形
四边形![]() 的面积,
的面积,
由(2)得四边形![]() 的面积
的面积![]() 四边形AECF的面积
四边形AECF的面积
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 的面积为
的面积为![]() ,
,
∴四边形![]() 的面积为
的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).
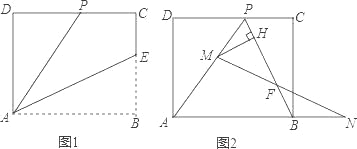
(1)求AB的长;
(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“学习强国”阅读知识竞赛中,每班参加比赛的人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分和
分和![]() 分.年级组长张老师将班
分.年级组长张老师将班![]() 和
和![]() 班的成绩进行整理并绘制成如下的统计图:
班的成绩进行整理并绘制成如下的统计图:
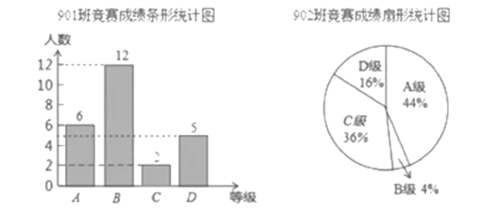
(1)在本次竞赛中,![]() 班
班![]() 级及以上的人数有多少?
级及以上的人数有多少?
(2)请你将下面的表格补充完整:
平均数(分) | 中位数(分) | 众数(分) |
| |
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
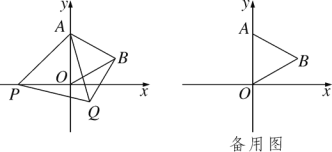
【题目】如图,在平面直角坐标系中,已知点A(0,4),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由;
(3)连接OQ,当OQ∥AB时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
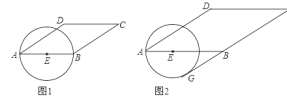
【题目】如图,在平行四边形ABCD中,AB=10(AB>AD),AD与BC之间的距离为6,点E在线段AB上移动,以E为圆心,AE长为半径作⊙E.
(1)如图1,若E是AB的中点,求⊙E在AD所在的直线上截得的弦长;
(2)如图2,若⊙E与BC所在的直线相切,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某中学数学活动小组为了调查居民的用水情况,从某社区的![]() 户家庭中随机抽取了
户家庭中随机抽取了![]() 户家庭的月用水量,结果如下表所示:
户家庭的月用水量,结果如下表所示:
月用水量(吨) |
|
|
|
|
|
|
|
户数 |
|
|
|
|
|
|
|
(1)求这![]() 户家庭月用水量的平均数、众数和中位数;
户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为![]() (吨),家庭月用水量不超过
(吨),家庭月用水量不超过![]() (吨)的部分按原价收费,超过
(吨)的部分按原价收费,超过![]() (吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一旅游团来到某旅游景点,看到售票处旁边的公告栏上写着:①一次购买10张以下(含10张),每张门票180元.②一次购买10张以上,超过10张的部分,每张门票6折优惠.
(1)若旅游团人数为9人,门票费用是多少?若旅游团人数为30人,门票费用又是多少?
(2)设旅游团人数为x人,写出该旅游团门票费用y(元)与人数x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水晶厂生产的水晶工艺品非常畅销,某网店专门销售这种工艺品.成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当x=40时,y=300;当x=55时,y=150.
(1)求y与x之间的函数关系式;
(2)如果规定每天工艺品的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该工艺品销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)读读做做:教材中有这样的问题,观察下面的式子,探索它们的规律,![]() =1-
=1-![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ……用正整数n表示这个规律是______;
……用正整数n表示这个规律是______;
(2)问题解决:一容器装有1L水,按照如下要求把水倒出:第一次倒出![]() L水,第二次倒出的水量是
L水,第二次倒出的水量是![]() L水的
L水的![]() ,第三次倒出的水量是
,第三次倒出的水量是![]() L水的
L水的![]() ,第四次倒出的水量是
,第四次倒出的水量是![]() L水的
L水的![]() ,……,第n+1次倒出的水量是
,……,第n+1次倒出的水量是![]() L水的
L水的![]() ,……,按照这种倒水方式,这1L水能否倒完?
,……,按照这种倒水方式,这1L水能否倒完?
(3)拓展探究:①解方程:![]() +
+![]() +
+![]() +
+![]() =
=![]() ;
;
②化简:![]() +
+![]() +
+![]() …+
…+![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com