
【题目】如图,已知抛物线y=ax2+bx+3过等腰Rt△BOC的两顶点B、C,且与x轴交于点A(﹣1,0).
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线BC相交于点M,点N为x轴上一点,当以M,N,B为顶点的三角形与△ABC相似时,求BN的长度;
(3)P为线段BC上方的抛物线上的一个动点,P到直线BC的距离是否存在最大值?若存在,请求出这个最大值的大小以及此时点P的坐标;若不存在,请说明理由.

【答案】(1)y=﹣x2+2x+3(2)3或![]() (3)
(3)![]()
【解析】
(1)令x=0,可得y=3,可得C点坐标为(0,3),根据等腰直角三角形的性质可得B点坐标为(3,0),即可利用待定系数法求得该抛物线的解析式.
(2)已知了B、C的坐标,易求得BC的长和直线BC的解析式,联立抛物线的对称轴即可得到点M的坐标,从而求得BM的长,可设出点BN=x,若以M,N,B为顶点的三角形与△ABC相似,由于∠CBA=∠MBN,则有两种情况需要考虑:①△MBN∽△CBA,②△MBN∽△ABC;根据上述两种情况所得不同的比例线段即可求得点N的坐标,进而可求出BN的长.
(3)可设经过P与直线BC平行的直线解析式为y=﹣x+n,联立方程y=﹣x2+2x+3,根据判别式为0得到n,从而得到经过P与直线BC平行的直线解析式,进一步得到点P的坐标,再根据待定系数法求得经过点P与直线BC垂直的直线解析式,联立直线BC的解析式得到交点坐标,再根据两点间的距离公式求解即可.
(1)令x=0,则y=3,∴C(0,3),∴OC=3.
又∵Rt△BOC是等腰直角三角形,∴B(3,0),将A(﹣1,0),B(3,0)代入y=ax2+bx+3得:![]() ,解得
,解得![]() ,∴y=﹣x2+2x+3.
,∴y=﹣x2+2x+3.
(2)抛物线的对称轴为直线x=﹣![]() =1,由B(3,0),C(0,3),得直线BC解析式为:y=﹣x+3;
=1,由B(3,0),C(0,3),得直线BC解析式为:y=﹣x+3;
∵对称轴x=1与直线BC:y=﹣x+3相交于点M,∴M为(1,2);
可设BN的长为x.
当△MNB∽△ACB时,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:x=3;
,解得:x=3;
当△MNB∽△CAB时,∴![]() =
=![]()
![]() =
=![]() ,解得:x=
,解得:x=![]() ,所以BN的长为3或
,所以BN的长为3或![]() .
.
(3)设经过P与直线BC平行的直线解析式为y=﹣x+n,联立得:![]() ,﹣x+n=﹣x2+2x+3,x2﹣3x+n﹣3=0,△=9﹣4(n﹣3)=0,解得:n=
,﹣x+n=﹣x2+2x+3,x2﹣3x+n﹣3=0,△=9﹣4(n﹣3)=0,解得:n=![]() ,∴P到直线BC的距离存在最大值时,经过P与直线BC平行的直线解析式为y=﹣x+
,∴P到直线BC的距离存在最大值时,经过P与直线BC平行的直线解析式为y=﹣x+![]() ,则x2﹣3x+
,则x2﹣3x+![]() =0,解得:x=
=0,解得:x=![]() ,y=﹣
,y=﹣![]() +
+![]() =
=![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ),则经过点P与直线BC垂直的直线解析式为y=x+t,则
),则经过点P与直线BC垂直的直线解析式为y=x+t,则![]() =
=![]() +t,解得:t=
+t,解得:t=![]() ,故经过点P与直线BC垂直的直线解析式为y=x+
,故经过点P与直线BC垂直的直线解析式为y=x+![]() ,联立可得
,联立可得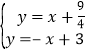 ,解得:
,解得: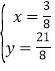 ,则P到直线BC的距离最大值为
,则P到直线BC的距离最大值为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A(2,4),B(4,1),C(-3,4)

(1)平移线段AB到线段CD,使点A与点C重合,写出点D的坐标.
(2)直接写出线段AB平移至线段CD处所扫过的面积.
(3)平移线段AB,使其两端点都在坐标轴上,则点A的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(2,4).

(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:
①在图中找一点P,使得P到AB、AC的距离相等,且PA=PB;
②在x轴上找一点Q,使得△QAB的周长最小,并求出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的爸爸在池边开了一块四边形土地种蔬菜,爸爸让小明计算一下土地的面积,以便计算产量.小明找了米尺和测角仪,测得AB=3米,BC=4米,CD=12米,DA=13米,∠B=90°.
⑴若连接AC,试证明:△ACD是直角三角形;
⑵请你帮小明计算这块土地的面积为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对下面数学模型的研究学习,解决下列问题:
(模型呈现)
(1)如图1,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .由
.由![]() ,得
,得![]() .又
.又![]() ,可以推理得到
,可以推理得到![]() .进而得到
.进而得到![]() _____,
_____,![]() _____.我们把这个数学模型称为“
_____.我们把这个数学模型称为“![]() 字”模型或“一线三等角”模型;
字”模型或“一线三等角”模型;
(模型应用)
(2)①如图2,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() .求证:点
.求证:点![]() 是
是![]() 的中点.
的中点.
②如图3,在平面直角坐标系![]() 中,点
中,点![]() 为平面内任一点,点
为平面内任一点,点![]() 的坐标为
的坐标为![]() .若
.若![]() 是以
是以![]() 为斜边的等腰直角三角形,请直接写出点
为斜边的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=6,则S1+S5=_____.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验中学为了解学生“最适合自己的考前减压方式”,在九年级范围内开展了一次抽样调查,学生必须在四类选项中选择一项,小明根据调查结果绘制了如下尚不完整的统计图.
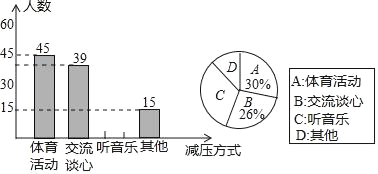
请根据以上信息解答下列问题:
(1)这次抽样调查中,抽查的学生人数为______人.
(2)请补全条形统计图.
(3)扇形统计图中“其他”所对应扇形圆心角为______度.
(4)若实验中学九年级有700人,请估计采用“听音乐”作为减压方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
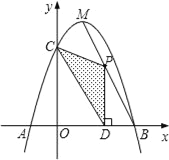
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,如取款、上网等都需要密码,有一种利用“因式分解”产生的密码,方便记忆,原理是:如多项式![]() ,若
,若![]() ,
,![]() 时,则各因式的值为
时,则各因式的值为![]() ,
,![]() ,
,![]() ,于是把018162作为一个六位数的密码,对于多项式
,于是把018162作为一个六位数的密码,对于多项式![]() ,取
,取![]() ,
,![]() 时,用上述方法产生的密码是_________________.(写一个即可)
时,用上述方法产生的密码是_________________.(写一个即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com