
����Ŀ���ۺ���ʵ��
�۲����

��ͼ1���й���ֱ�Ƕ���![]() ��������ȫ�ȵĵ���ֱ�����dzߵ�����һ�𣬵�
��������ȫ�ȵĵ���ֱ�����dzߵ�����һ�𣬵�![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��.
��.
��1����ͼ1�У��㷢���߶�![]() ��
��![]() ��������ϵ��___________��ֱ��
��������ϵ��___________��ֱ��![]() ��
��![]() ��λ�ù�ϵ��________.
��λ�ù�ϵ��________.
��������
��2����ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ����ǵõ�ͼ2����ʱ��1���е����������Ƿ�����������жϲ�˵�����ɣ�
��ʱ����תһ����ǵõ�ͼ2����ʱ��1���е����������Ƿ�����������жϲ�˵�����ɣ�
�ع�̽��
��3����ͼ3����ֻ�����й���ֱ�Ƕ���![]() ��������ȫ�ȵĵ���ֱ�����dz�����Ϊ���й�������Ϊ
��������ȫ�ȵĵ���ֱ�����dz�����Ϊ���й�������Ϊ![]() ����ǣ���������ȫ�ȵ�������������
����ǣ���������ȫ�ȵ�������������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת����һ����ǣ���ʱ��1���е�����������Ȼ�����������жϣ�����˵������.
��ʱ����ת����һ����ǣ���ʱ��1���е�����������Ȼ�����������жϣ�����˵������.
���𰸡���1��![]() ��
��![]() ����2����ͼ1�е�
����2����ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ�����ʱ���������۳���.���ɼ���������3������
��ʱ����תһ�����ʱ���������۳���.���ɼ���������3������![]() ����������
����������![]() ������.
������.
��������
��1�����ݡ�ABC�͡�ADE�ǵ���ֱ�������Σ��õ�AB=AC��AD=AE����A=90�㣬���ɵó����ۣ�
��2������ת�����ʵõ���DAB=��EAC������SAS֤����ABD�ա�ACE������ȫ�������εĶ�Ӧ����ȵó�BD=CE���ӳ�DB����CE�ڵ�F����AE�ڵ�O����ȫ�������ζ�Ӧ����ȵõ���ADB=��AEC�������������ڽǺͶ����ͶԶ�����ȣ��õ���OFE=��OAD=90�㣬���ɵó����ۣ�
��3�����ƣ�2���ɵ�BD=CE������BD��CE��������
��1���ߡ�ABC�͡�ADE�ǵ���ֱ�������Σ���AB=AC��AD=AE����A=90�㣬��BD=CE��BD��CE��
�ʴ�Ϊ��BD=CE��BD��CE��
��2����ͼ1�еġ�ABC�Ƶ�A��ʱ����תһ�����ʱ���������۳������������£�
����ת�ã���DAB=��EAC��
�֡�AB=AC��AD=AE��
���ABD�ա�ACE��SAS����
��BD=CE��
��ͼ���ӳ�DB����CE�ڵ�F����AE�ڵ�O��
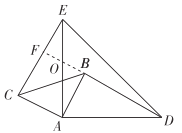
�ߡ�ABD�ա�ACE��
���ADB=��AEC��
�ߡ�AOD=��EOF��
���OFE=��OAD��
�ߡ�OAD=90�㣬
���DFE=90�㣬��BD��CE��
��3������BD=CE����������BD��CE���������������£�
����ת�ã���DAE=��BAC��
���DAB=��EAC��
�֡�AB=AC��AD=AE��
���ABD�ա�ACE��SAS����
��BD=CE��
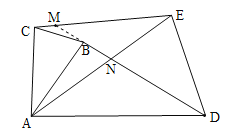
�ӳ�DB��CE��M��BD��AE���ڵ�N��
�ߡ�ABD�ա�ACE�����MEA=��BDA��
�ߡ�ENM=��DNA�����EMN=��EAD��
�ߡ�EAD��90�㣬���EMN��90�㣬��BD��CE��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���3��15����������������Ȩ������������Ҿ��̳Ƕ�����������������д��۴����.�����ҵ�A��Ʒ�ɱ�Ϊ600Ԫ���ڱ��1000Ԫ�Ļ����ϴ�8������.
��1�����ڼ�����������������������������ཱུ�۶���Ԫ������ʹ�����ʲ�����20%��
��2����ý�屬�ϣ���һЩ�����������Ʒ�۸���ٽ��۴�����������թ��Ϊ.������Ҳ����A��Ʒ����ɱ�������������һ�£���ǰÿ�ܿ��۳�50�������������Ƚ�������2m%���ٴ������24mԪ��ʹ��A��Ʒ��3��15����һ�������������ͱ�ԭ��һ������������������ ![]() m%������һ�������ﵽ��20000Ԫ����m��ֵ.
m%������һ�������ﵽ��20000Ԫ����m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ÿǧ��30Ԫ�ļ۸�һ��ԭ���ϼӹ�����ۣ����������֣�ÿ���������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�����һ�κ���y��kx+b����x��35ʱ��y��55��x��42ʱ��y��48��
��1����һ�κ���y��kx+b�ı���ʽ��
��2������̻�ÿ���õ���������ΪW��Ԫ�����������W��Ԫ�������۵���x��Ԫ/ǧ�ˣ�֮��Ĺ�ϵʽ��
��3�����۵���ÿǧ�˶�Ϊ����Ԫʱ���̻�ÿ��ɻ�����������������Ƕ���Ԫ���������������۶�ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� Ϊ��������̼����������ѡ�������г���Ϊ�������ߣ���ͼ1��ʾ��һ�����г���ʵ��ͼ�����ܵ�AC��CD�ij��ֱ�Ϊ45cm��60cm�������ǻ��ഹֱ������CE�ij�Ϊ20cm����A��C��E��ͬһ��ֱ���ϣ�����CAB=75������ͼ2��
��1���ܵ�AD�ij���
��2��������E�����ܵ�AB�ľ��룮
(�����ȷ��1 cm���ο����ݣ� sin75��="0.966," cos75��=0.259��tan75��=3.732)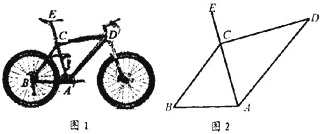
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
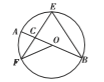
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ��
��![]() ���ң���
���ң���![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ����
����![]() ����
����![]() �Ķ����ǣ� ��
�Ķ����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ�����۳�20����ÿ��ӯ��40Ԫ�������鷢�֣�������ֳ������ۼ�ÿ����1Ԫʱ��ƽ��ÿ���ܶ��۳�2��.��ÿ����������xԪ.
��1�����ۺ�ÿ������������Ϊ_____Ԫ������Ϊ_____�������ú�x��ʽ�ӱ�ʾ��
��2��Ϊ���������ۣ�������ٿ�棬�̳������ȡ���۴�ʩ������Ҫƽ��ÿ��ӯ��1200Ԫ����ÿ������Ӧ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ����б��Ϊ![]() ��б�µĺ���棬
��б�µĺ���棬![]() ��б�¶���B�����ľ���
��б�¶���B�����ľ���![]() Ϊ3�ף�Ϊ�˶����б���ϵ��̵ؽ�����࣬��б�µ˰�װ��һ����ͷA����ͷA�����ˮ���ڿ����߹������߿��Կ��������ߵ�һ���֣������ˮ�����ֱ�߶�Ϊy����λ���ף���ˮ�����ֱ�߶���ָˮ�������ľ��룩��ˮ������ͷA��ˮƽ����Ϊx����λ���ף���y��x֮��������㺯����ϵ
Ϊ3�ף�Ϊ�˶����б���ϵ��̵ؽ�����࣬��б�µ˰�װ��һ����ͷA����ͷA�����ˮ���ڿ����߹������߿��Կ��������ߵ�һ���֣������ˮ�����ֱ�߶�Ϊy����λ���ף���ˮ�����ֱ�߶���ָˮ�������ľ��룩��ˮ������ͷA��ˮƽ����Ϊx����λ���ף���y��x֮��������㺯����ϵ![]() ��a��b�dz�����
��a��b�dz�����![]() ����ͼ2��¼��x��y��������ݣ�
����ͼ2��¼��x��y��������ݣ�
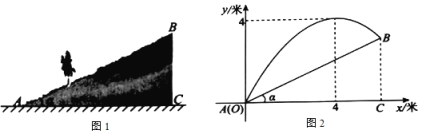
��1����y����x�ĺ�����ϵʽ��
��2��б������һ�ø�1.8������������ͷA��ˮƽ����Ϊ2�ף�ͨ�������жϴ�A�����ˮ���ܷ�Խ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��У����ȫ�ǽ���������ע���ش����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ��ѧ�С����������¼�·����ʻ�������ٶȵ�ʵ�飺���ڹ�·�Ա�ѡȡһ��C�����ڱ�ֱ�ij���![]() ��ȷ����D��ʹCD��
��ȷ����D��ʹCD��![]() ��ֱ�����CD�ij�����21������
��ֱ�����CD�ij�����21������![]() �ϵ�D��ͬ��ȡ��A��B��ʹ��CAD=300����CBD=600��
�ϵ�D��ͬ��ȡ��A��B��ʹ��CAD=300����CBD=600��
(1)��AB�ij�(��ȷ��0.1�����ο����ݣ�![]() )��
)��
(2)��֪��·�ζ�У������Ϊ40ǧ�ף�Сʱ�������ij��У����A��B��ʱ2�룬����У���Ƿ���?˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90����AC=2��BC=4��CD����ABC�����ߣ�E�DZ�BC��һ���㣬����BED��ED�۵�����B���ڵ�F����EF���߶�CD�ڵ�G������DFG��ֱ��������ʱ����CE=__________.
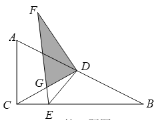
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com