
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 是
是![]() 的弦,且
的弦,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
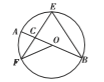
连接OE、FB.在△EFO中,由等边对等角得到∠FEO的度数,证明△EFO≌△EBO,得到∠BEO=∠FEO,从而得到∠FEB的度数.在△EFB中,根据等边对等角和三角形内角和定理得出∠EFB的度数,进而得到∠OFB的度数.在△OFB中,根据等边对等角得出∠OBF的度数,根据圆周角定理即可得到∠AOF的度数.
连接OE、FB.
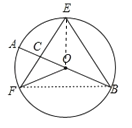
∵OF=OE,∴∠FEO=∠EFO=35°.
在△EFO和△EBO中,∵EF=BE,OE=OE,OF=OB,
∴△EFO≌△EBO,∴∠BEO=∠FEO=35°,∴∠FEB=70°.
∵EF=EB,∴∠EFB=∠EBF=(180°-70°)÷2=55°,∴∠OFB=∠EFB-∠EFO=55° -35°=20°.
∵OF=OB,∴∠OBF=∠OFB=20°,∴∠AOF=2∠OBF=40°.
故选C.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,小明利用所学数学知识测量某建筑物BC高度,采用了如下的方法:小明从与某建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走260米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为72°,建筑物底端B的俯角为63°,其中点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据小明的测量数据,计算得出建筑物BC的高度约为( )米(计算结果精DE确到0.1米,参考数据:sin72°≈0.95,tan72°≈3.08,sin63°≈0.89,tan63°≈1.96)
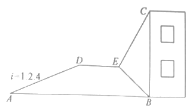
A.157.1 B.157.4 C.257.4 D.257.1
查看答案和解析>>
科目:初中数学 来源: 题型:
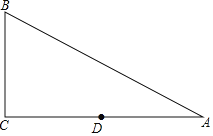
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是![]() 时,△DEF腰长的值是_____.
时,△DEF腰长的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师为了了解学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半年的跟踪调查,并将调查结果分成四类A:优;B:良;C:中;D:差.依据调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
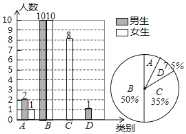
(1)本次调查中,周老师一共调查了______名学生;
(2)将统计图补充完整;
(3)为了共同进步,周老师想从被调查的A类和D类学生中分别选取一位同学进行“一对一”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
观察猜想

如图1,有公共直角顶点![]() 的两个不全等的等腰直角三角尺叠放在一起,点
的两个不全等的等腰直角三角尺叠放在一起,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.
(1)在图1中,你发现线段![]() ,
,![]() 的数量关系是___________,直线
的数量关系是___________,直线![]() ,
,![]() 的位置关系是________.
的位置关系是________.
操作发现
(2)将图1中的![]() 绕点
绕点![]() 逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
拓广探索
(3)如图3,若只把“有公共直角顶点![]() 的两个不全等的等腰直角三角尺”改为“有公共顶角为
的两个不全等的等腰直角三角尺”改为“有公共顶角为![]() (锐角)的两个不全等等腰三角形”,
(锐角)的两个不全等等腰三角形”,![]() 绕点
绕点![]() 逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .
.

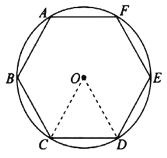
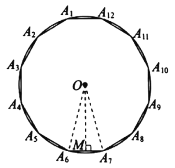
刘徽从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割的越细,圆的内接正多边形就越接近圆.设圆的半径为R,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;请写出圆内接正二十四边形的周长
;请写出圆内接正二十四边形的周长![]() ________,计算
________,计算![]() ________.(参考数据:
________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
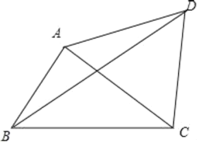
【题目】如图,在△ABC中,以AC为边向外作等边△ACD.
(1)画出将△ABD绕点A顺时针旋转60°后得到的△ACE;
(2)若∠ABC=60°,AB=3,BC=5,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com