
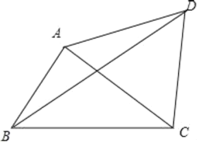
【题目】如图,在△ABC中,以AC为边向外作等边△ACD.
(1)画出将△ABD绕点A顺时针旋转60°后得到的△ACE;
(2)若∠ABC=60°,AB=3,BC=5,求BD的长.
【答案】(1)见解析;(2)7
【解析】
(1)根据旋转变换的定义和性质作图可得;
(2)连接BE,过点E作EF⊥BC,交CB延长线于点F,先证△ABE为等边三角形得AB=AE=BE=3,∠ABE=60°,由∠ABC=60°知∠EBF=60°,据此知BF=BEcos60°=![]() ,EF=BEsin60°=
,EF=BEsin60°=![]() ,根据勾股定理可得EC=7,再证△EAC≌△BAD得BD=CE=7.
,根据勾股定理可得EC=7,再证△EAC≌△BAD得BD=CE=7.
解:(1)如图所示,△ACE即为所求.
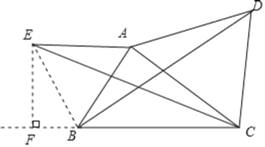
(2)如图,连接BE,过点E作EF⊥BC,交CB延长线于点F,
∵∠BAE=∠CAD=60°,AE=AB,
∴△ABE是等边三角形,
∴AB=AE=BE=3,∠ABE=60°,
∵∠ABC=60°,
∴∠EBF=60°,
∴BF=BEcos60°=![]() ,EF=BEsin60°=
,EF=BEsin60°=![]() ,
,
则EC=![]() =
=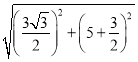 =7,
=7,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠EAC=∠BAD,
∴△EAC≌△BAD(SAS),
∴BD=CE=7.


科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个倾斜角为![]() 的斜坡的横截面,
的斜坡的横截面,![]() .斜坡顶端B与地面的距离
.斜坡顶端B与地面的距离![]() 为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系
为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系![]() (a,b是常数,
(a,b是常数,![]() ),图2记录了x与y的相关数据.
),图2记录了x与y的相关数据.
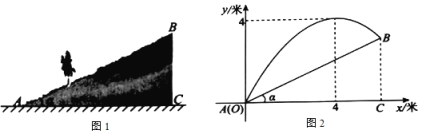
(1)求y关于x的函数关系式;
(2)斜坡上有一棵高1.8米的树,它与喷头A的水平距离为2米,通过计算判断从A喷出的水珠能否越过这棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店进口一种高档水果,卖出每斤水果盈利(毛利润)5元,每天可卖出1000斤,经市场调査后发现,在进价不变的情况下,若每斤售价涨0.5元,每天销量将减少40斤.
(1)若以每斤盈利9元的价钱出售,问每天能盈利多少元?
(2)若水果店要保证每天销售这种水果的毛利润为6000元,同时又要使顾客觉得价不太贵,则每斤水果应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
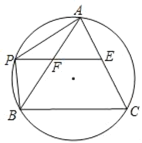
【题目】如图,等边三角形ABC中,E、F为AC、AB中点,EF延长线交△ABC外接圆于P,则PB:AP的数值为_____(提示:圆内接四边形对角互补)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,
OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的![]() ,那么点B′的坐标是【 】
,那么点B′的坐标是【 】

A.(-2,3) B.(2,-3) C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com