
【题目】如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=x,⊙O的半径为y,求y与x的函数关系式.
【答案】
(1)
解:(1)连接OE,OD,

在△ABC中,∠C=90°,AC+BC=8,
∵AC=2,
∴BC=6;
∵以O为圆心的⊙O分别与AC,BC相切于点D,E,
∴四边形OECD是正方形,
tan∠B=tan∠AOD=![]() ,解得OD=
,解得OD=![]() ,
,
∴圆的半径为![]() ;
;
(2)
解:∵AC=x,BC=8﹣x,
在直角三角形ABC中,tanB=![]() ,
,
∵以O为圆心的⊙O分别与AC,BC相切于点D,E,
∴四边形OECD是正方形.
tan∠AOD=tanB=![]() ,
,
解得y=﹣![]() x2+x.
x2+x.
【解析】(1)根据切线,连接圆心和切点求半径。
(2)构造直角三角形,利用三角函数建立方程即可得解析式。
【考点精析】通过灵活运用三角形的面积和切线的性质定理,掌握三角形的面积=1/2×底×高;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张卡片(形状、大小、颜色、质地都相等),正面分别写上整式x2+1,﹣x2﹣2,3.将这三张卡片背面向上洗匀,从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式![]() .
.
(1)请用画树状图或列表的方法,写出代数式![]() 所有可能的结果;
所有可能的结果;
(2)求代数式![]() 恰好是分式的概率.
恰好是分式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y=![]() 图象经过点A.
图象经过点A.
(1)求k的值
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,试判断点D是否在该反比例函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长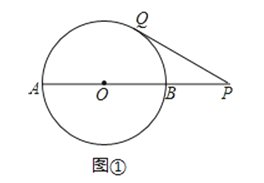
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.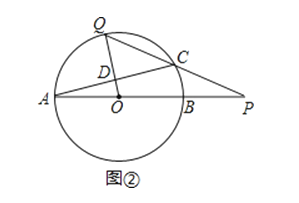
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么点
(2,0),…那么点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com