
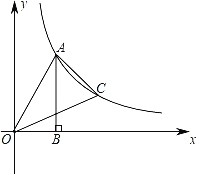
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=
(x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=![]() .点C是反比例函数y=
.点C是反比例函数y=![]() (x>0)图象上一动点,连接AC,OC,若△AOC的面积为
(x>0)图象上一动点,连接AC,OC,若△AOC的面积为![]() ,则点C的坐标为_____.
,则点C的坐标为_____.
【答案】(4,![]() ).
).
【解析】
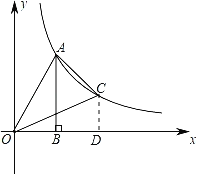
作CD⊥x轴于D,解直角三角形求得A(2,5),设点C的坐标为(m,![]() ),根据S△AOC=S△AOB+S梯形ABDC﹣S△COD=S梯形ABDC,得出
),根据S△AOC=S△AOB+S梯形ABDC﹣S△COD=S梯形ABDC,得出![]() (5+
(5+![]() )(m﹣2)=
)(m﹣2)=![]() ,解得m=4,即可求得C点的坐标.
,解得m=4,即可求得C点的坐标.
解:作CD⊥x轴于D,
∵点A是反比例函数y=![]() (x>0)图象上一点,设A(x,
(x>0)图象上一点,设A(x,![]() ),
),
∴OB=x,AB=![]() ,
,
∵tan∠OAB=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得x=2,
,解得x=2,
∴A(2,5)
设点C的坐标为(m,![]() )
)
∵S△AOC=S△AOB+S梯形ABDC﹣S△COD=S梯形ABDC,△AOC的面积为![]() ,
,
∴![]() (AB+CD)BD=
(AB+CD)BD=![]() ,
,
∴![]() (5+
(5+![]() )(m﹣2)=
)(m﹣2)=![]() ,
,
整理得,m2﹣3m﹣4=0,
解得m=4或m=﹣1(舍去),
∴点C的坐标为(4,![]() ),
),
故答案为(4,![]() ).
).


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
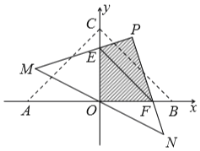
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,点
,点![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转(旋转角为锐角),得
顺时针旋转(旋转角为锐角),得![]() ,
,![]() 、
、![]() 、
、![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)求四边形![]() 的面积;
的面积;
(2)设![]()
![]() ,
,![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,当
,当![]() 的值最小时,求
的值最小时,求![]() 的坐标.(直接写出结果)
的坐标.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
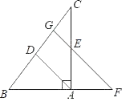
【题目】如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过AC的中点E作FG∥AD,交BA的延长线于点F,交BC于点G,
(1)求证:AE=AF;
(2)若BC=![]() AB,AF=3,求BC的长.
AB,AF=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一个动点,作
上一个动点,作![]() ,交直角边
,交直角边![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .连结
.连结![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)求证:![]() ;
;
(3)如图2,当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的直径;
的直径;
(4)若以![]() 为顶点的三角形是等腰三角形时,求所有满足条件的
为顶点的三角形是等腰三角形时,求所有满足条件的![]() 的值.
的值.
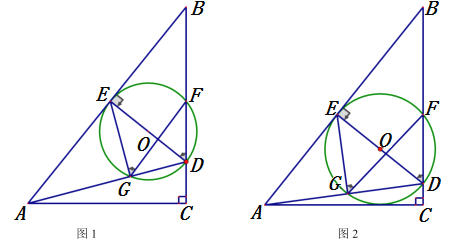
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把函数![]() 的图像绕点
的图像绕点![]() 旋转180°,得到新函数
旋转180°,得到新函数![]() 的图像,我们称
的图像,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图像的对称轴为直线
的图像的对称轴为直线![]() .例如:当
.例如:当![]() 时,函数
时,函数![]() 关于点
关于点![]() 的相关函数为
的相关函数为![]() .
.
(1)填空:![]() 的值为________(用含
的值为________(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,
时,![]() 的图像与
的图像与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 绕原点
绕原点![]() 顺时针旋转90°,得到它的对应线段
顺时针旋转90°,得到它的对应线段![]() .若线段
.若线段![]() 与
与![]() 的图像有公共点,结合函数图像,求
的图像有公共点,结合函数图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动公司为了提升“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底
的距离为3.9米.同时为了提醒市民,在距离斜坡底![]() 点4.4米的水平地面上立了一块警示牌
点4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成
.当太阳光线与水平线成![]() 角时,测得信号塔
角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(结果精确到十分位,参考数据:
的高约为(结果精确到十分位,参考数据:![]() ,
,![]() ,
,![]() )
)
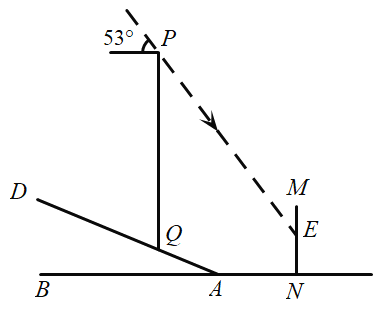
A.11.9米B.10.4米C.11.4米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
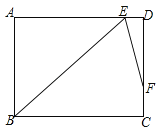
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:![]() ≈1.732)
≈1.732)
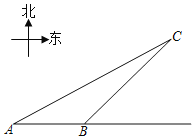
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com