
【题目】(1)阅读并回答:科学实验证明,平面镜反射的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2, ∠3=∠4.
①由条件可知:∠1与∠3的大小关系是_____,∠2与∠4的大小关系是________;
②反射光线BC与EF的位置关系是___________,理由是___________;
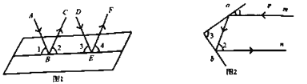
(2)解决问题:①如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=35°,则∠2=_______,∠3=_______;
②在①中,若∠1=40°,则∠3=_______,
③由①②请你猜想:当∠3=_______时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
【答案】(1)①相等;相等②平行,理由是同位角相等,两直线平行;(2)①∠2=70°70°,∠3=90°;②∠3=90°;③猜想:当∠3=90°时,m总平行于n,理由见解析.
【解析】
(1)根据平行线的判定与性质逐一求解可得;
(2)①根据入射角等于反射角得出∠1=∠4,∠5=∠7,求出∠6,根据平行线性质即可求出∠2,求出∠5,根据三角形内角和求出∠3即可;
②与①同理;
③求出∠4+∠5,求出∠1+∠4+∠5+∠7,即可求出∠2+∠6,根据平行线的判定推出即可.
解:(1)①由条件可知:∠1与∠3的大小关系是相等,理由是两直线平行,同位角相等;∠2与∠4的大小关系是相等;
②反射光线BC与EF的位置关系是平行,理由是同位角相等,两直线平行;
故答案为:①相等、两直线平行,同位角相等、相等;②平行、同位角相等,两直线平行.
(2)①如图,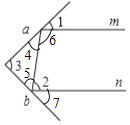
∵∠1=35°,
∴∠4=∠1=35°,
∴∠6=180°-35°-35°=110°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=70°,
∴∠5=∠7=55°,
∴∠3=180°-55°-35°=90°;
②在①中,若∠1=40°,则∠4=∠1=40°,
∴∠6=180°-40°-40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7=50°,
∴∠3=180°-50°-40°=90°
③猜想:当∠3=90°时,m总平行于n,
理由:∵三角形的内角和为180°,又∠3=90°,
∴∠4+∠5=90°
∵∠4=∠1、∠5=∠7,
∴∠1+∠7=90°,
∴∠1+∠4+∠5+∠7=90°+90°=180°,
∵∠1+∠4+∠6+∠5+∠2+∠7=180°+180°=360°,
∴∠6+∠2=180°
∴m∥n(同旁内角互补,而直线平行)
故答案为:①70°、90°;②90°;③90°.


科目:初中数学 来源: 题型:
【题目】某校为了解本校中考体育备考情况,随机抽去九年级部分学生进行了一次测试(满分60分,成绩均记为整数分)并按测试成绩(单位:分)分成四类:A类(54≤a≤60),B类(48≤a≤53),C类(36≤a≤47),D类(a≤35)绘制出如下两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)请补全统计图;
(2)在扇形统计图汇总,表示成绩类别为“C”的扇形所对应的圆心角是度;
(3)该校准备召开体育考经验交流会,已知A类学生中有4人满分(男生女生各有2人),现计划从这4人中随机选出2名学生进行经验介绍,请用树状图或列表法求所抽到的2,名学生恰好是一男一女的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)请值接写出点A,B,C的坐标.
(2)若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯距地面8米,身高1.6米的小明从距离灯底(点O)20米的点A处,沿AO所在直线行走12米到达点B时,小明身影长度( )
A.变长2.5米
B.变短2米
C.变短2.5米
D.变短3米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:
①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤S四边形AEPF= ![]() S△ABC .
S△ABC .
当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过平移,△ABC移到△DEF的位置,如图,下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF.正确的有( )
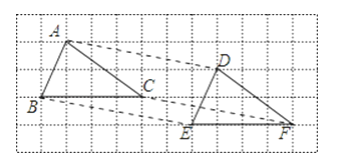
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() ,甲、乙两人从两地出发相向而行,甲先出发。图中
,甲、乙两人从两地出发相向而行,甲先出发。图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系,结合图象回答下列问题:
的关系,结合图象回答下列问题:
(1)表示甲离![]() 地的距离与时间关系的图象是_____(填
地的距离与时间关系的图象是_____(填![]() 或
或![]() ),甲的速度是__________
),甲的速度是__________![]() ,乙的速度是____________
,乙的速度是____________![]() 。
。
(2)甲出发后多少时间两人恰好相距![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…
(1)观察图形并完成表格:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图n中,菱形的个数为 [用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() (x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( )
(x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( ) 
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com