
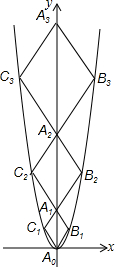
 二次函数y=$\sqrt{3}$x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点C1,C2,C3,…,Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An-1BnAn=120°.则A1的坐标为(0,2$\sqrt{3}$);菱形An-1BnAnCn的边长为2n.
二次函数y=$\sqrt{3}$x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点C1,C2,C3,…,Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An-1BnAn=120°.则A1的坐标为(0,2$\sqrt{3}$);菱形An-1BnAnCn的边长为2n. 分析 由于△A0B1A1,△A1B2A2,△A2B3A3,…,都是等边三角形,因此∠B1A0x=30°,可先设出△A0B1A1的边长,然后表示出B1的坐标,代入抛物线的解析式中即可求得△A0B1A1的边长,用同样的方法可求得△A0B1A1,△A1B2A2,△A2B3A3,…的边长,然后根据各边长的特点总结出此题的一般化规律,根据菱形的性质易求菱形An-1BnAnCn的周长.
解答 解:∵四边形A0B1A1C1是菱形,∠A0B1A1=120°,
∴△A0B1A1是等边三角形.
设△A0B1A1的边长为m1,则B1(m1,$\sqrt{3}$m1);
代入抛物线的解析式中得:(m1)2=$\sqrt{3}$m1,
解得m1=0(舍去),m1=1;
故△A0B1A1的边长为2,
A1的坐标为(0,2$\sqrt{3}$),
同理可求得△A1B2A2的边长为4,
…
依此类推,等边△An-1BnAn的边长为2n,
故答案是:(0,2$\sqrt{3}$),2n.
点评 本题考查了菱形的性质,二次函数图象上点的坐标特征,等边三角形的判定与性质等知识点.解答此题的难点是推知等边△An-1BnAn的边长为2n.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
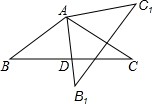 已知,如图,在△ABC中,AB=AC,AD是BC边上的中线,将△ABC绕点A按逆时针方向旋转,边AB落在直线AD上得到△AB1C1,求证:B1C1⊥AC.
已知,如图,在△ABC中,AB=AC,AD是BC边上的中线,将△ABC绕点A按逆时针方向旋转,边AB落在直线AD上得到△AB1C1,求证:B1C1⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
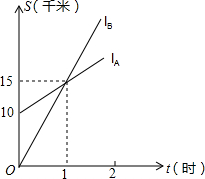 如图,lA、lB分别表示小明步行与小刚骑车在同一条路上行驶的路程S与时间t之间的关系.
如图,lA、lB分别表示小明步行与小刚骑车在同一条路上行驶的路程S与时间t之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 各角对应相等 | B. | 各边对应成比例 | ||
| C. | 各角对相等,各边对应相等 | D. | 各角对应相等,各边对应成比例 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=-2,x2=-3 | B. | x1=2,x2=3 | C. | x1=-6,x2=1 | D. | x1=6,x2=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com