
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地立即以另一速度按原路匀速返回到
地立即以另一速度按原路匀速返回到![]() 地;乙车匀速前往
地;乙车匀速前往![]() 地,设甲、乙两车距离
地,设甲、乙两车距离![]() 地的距离为
地的距离为![]() . 甲车行驶的时间为
. 甲车行驶的时间为![]() ,
,![]() 与
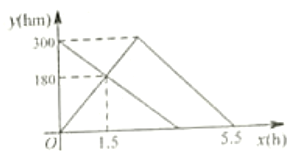
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲车从![]() 地前往
地前往![]() 地的速度为_______
地的速度为_______![]() .
.
(2)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)当甲、乙两车相距![]() 时,直接写出甲车行驶的时间.
时,直接写出甲车行驶的时间.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
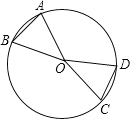
【题目】如图,OA,OB,OC,OD是⊙O的半径,
(1)如果∠AOB=∠COD,那么_______,_____=______,∠AOC______∠BOD;
(2)如果AB=CD,那么_____=_____,______;
(3)如果![]() =
=![]() ,那么____,_____,
,那么____,_____,![]() ______
______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
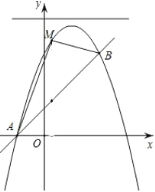
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?
查看答案和解析>>
科目:初中数学 来源: 题型:
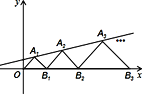
【题目】如图,在平面直角坐标系中,点A1,A2,A3,… 和B1,B2,B3,… 分别在直线![]() 和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解某学校大班额现状,某市决定通过新建学校来解决该问题.经测算,建设6个小学,5个中学,需费用13800万元,建设10个小学,7个中学,需花费20600万元.
(1)求建设一个小学,一个中学各需多少费用.
(2)该市共计划建设中小学80所,其中小学的建设数量不超过中学建设数量的1.5倍.设建设小学的数量为x个,建设中小学校的总费用为y万元.
①求y关于x的函数关系式;
②如何安排中小学的建设数量,才能使建设总费用最低?
(3)受国家开放二胎政策及外来务工子女就读的影响,预计在小学就读人数会有明显增加,现决定在(2)中所定的方案上增加投资以扩大小学的就读规模,若建设小学总费用不超过建设中学的总费用,则每所小学最多可增加多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为______cm2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com