
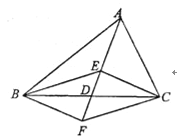
【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若AB=AC,求证:四边形BFCE是菱形.
【答案】(1)△BDF≌△EDC;(2)四边形BFCE是菱形.
【解析】试题分析:(1)由CE、BF的内错角相等,可得出△CED和△BFD的两组对应角相等;已知D是BC的中点,即BD=DC,由AAS即可证得两三角形全等;
(2)若AB=AC,则△ABC是等腰三角形,而D是底边BC的中点,根据等腰三角形三线合一的性质可证得AD⊥BC;由(1)的全等三角形,易证得四边形BFCE的对角线互相平分;根据对角线互相垂直平分的四边形是菱形即可判定四边形BFCE是菱形.
试题解析:(1)∵CE∥BF,
∴∠ECD=∠FBD,∠DEC=∠DFB;
又∵D是BC的中点,即BD=DC,
∴△BDF≌△EDC(AAS)
(2)∵AB=AC,
∴△ABC是等腰三角形;
又∵BD=DC,∴AD⊥BC(三线合一),
由(1)知:△BDF≌△EDC,
则DE=DF,DB=DC;
∴四边形BFCE是菱形(对角线互相平分且互相垂直的四边形为菱形).


科目:初中数学 来源: 题型:
【题目】若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定四边形是正方形的是( )
A. 对角线互相垂直且相等的四边形B. 一条对角线平分一组对角的矩形
C. 对角线相等的菱形D. 对角线互相垂直的矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组数:1.-2.3.-4.5.-6.7.-8.…,则第101个数是( )
A. 100 B. -100 C. 101 D. -101
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动课堂教学改革,打造“高效课堂”,我市某中学对该校八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图,请根据图中提供的信息,回答下列问题:
(1)本次调查的八年级部分学生共有______名;请补全条形统计图;
(2)若该校八年级学生共有540人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com