
【题目】某商场经营一批进价2元一件的小商品,在市场销售中发现此商品日销售单价x(元)与日销售量y(件)之间有如下关系:
x | 3 | 5 | 9 | 11 |
y | 18 | 14 | 6 | 2 |
(1)猜想日销售量y(件)与日销售单价x(元)之间可能存在怎样函数关系式?用你所学知识确定y与x之间的函数关系式,并验证你的猜想。
(2)设经营此商品的日销售利润为P(元),根据日销售规律:
①试求出日销售利润P(元)与日销售单价x之间的关系式,并求出日销售单价x为多少时,才能获得最大日销售利润,最大日销售利润为多少元?
②分别写出x和P的取值范围。
【答案】(1)y与x是一次函数关系;(2)①日销售利润获得最大值,为50元,②x≥0,-48≤P≤50
【解析】分析:(1)根据题意设出销售量y件与日销售单价x元之间的函数表达式,然后根据题目中的数据即可求得函数解析式;
(2)①根据题意和(1)中的函数解析式即可用含x的代数式表示出P,然后将P的关系式化为顶点式即可解答本题.②由实际情况得x≥0,结合关系式可求出P的取值范围.
详解:(1)∵y与x是一次函数关系,
∴设此直线的解析式为y=kx+b,
则由A(3,18),B(5,14),得
![]() ,解得
,解得![]() ,
,
∴y=-2x+24,
将C(9,6)D(11,2)代入y=-2x+24中验证,
满足这个解析式
∴y=-2x+24(0≤x<12),且x=12时,y=0.
(2)①P=y(x-2)=(-2x+24)(x-2)=-2![]() ,
,
当x=7时,日销售利润获得最大值,为50元。
②X的取值范围为x≥0, P的取值范围为 -48≤P≤50.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】小明同学为了解自己居住的小区家庭生活用水情况,从中随机调查了其中![]() 的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.
的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.
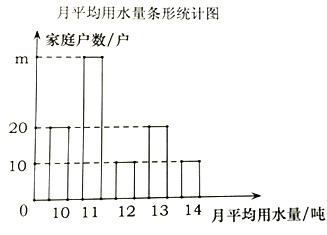
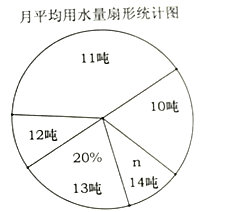
![]() 小明随机调查了 户家庭,该小区共有 户家庭;
小明随机调查了 户家庭,该小区共有 户家庭;
![]()
![]() ,
,![]() ;
;
![]() 这个样本数据的众数是 ,中位数是 ;
这个样本数据的众数是 ,中位数是 ;
![]() 根据样本数据,请估计该小区家庭月平均用水量不超过
根据样本数据,请估计该小区家庭月平均用水量不超过![]() 吨的有多少户?
吨的有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
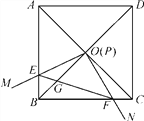
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:(1)EF=![]() OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OG·BD=AE2+CF2,其中正确的是__.
;(5)OG·BD=AE2+CF2,其中正确的是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴交于负半轴,给出六个结论:①a>0;②b>0;③c>0;④a+b+c=0;⑤b2﹣4ac>0;⑥2a﹣b>0,其中正确结论序号是_____.
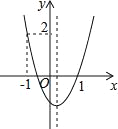
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点 E.若AB=8,BC=14,则线段EF的长为( )
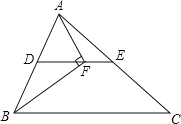
A. 2B. 3C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
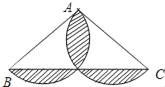
A. ![]() -24 B. 25π﹣24 C. 25π﹣12 D.
-24 B. 25π﹣24 C. 25π﹣12 D. ![]() -12
-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com