
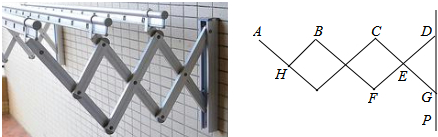
分析 (1)连接CD,由已知条件中CE=DE,∠CED=60°可知△CED为等边三角形,从而得出CD的长度;
(2)由图可知AD=3CD,由(1)可得知∠CED=60°时AD的长度;当∠CED=120°时,过点E作EH⊥CD于H,在Rt△CEH中用特殊角的三角函数值可求出CH的长度,从而得出CD和AD的长度.
解答 解:(1)连接CD,如图1所示.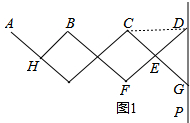
∵CE=DE=20cm,∠CED=60°,
∴△CED是等边三角形,
∴CD=DE=20cm.
故答案为:20cm.
(2)过点E作EH⊥CD于点H,如图2所示.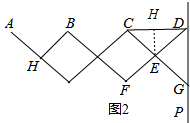
根据题意得:AB=BC=CD,
当∠CED=60°时,AD=3CD=60cm;
当∠CED=120°时,∠CEH=60°,CH=HD,
在Rt△CEH中,sin∠CEH=$\frac{CH}{CE}$,
∴CH=20sin60°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$(cm),
∴CD=20$\sqrt{3}$(cm),
∴AD=3×20$\sqrt{3}$=60$\sqrt{3}$≈103.8(cm),
∴103.8-60=43.8(cm),即点A向左移动了43.8cm.
故答案为:43.8cm.
点评 本题考查了等边三角形的判定及性质、解直角三角形以及特殊角的三角函数值,解题的关键:(1)找出△CED为等边三角形;(2)在Rt△CEH中利用特殊角的三角函数值求边的长度.本题属于中档题,难度不大,本题与现实生活联系紧密,是数学知识应用到实际的一个很好的案例.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1<x2<x3 | B. | x3<x1<x2 | C. | x3<x2<x1 | D. | x2<x1<x3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
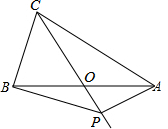 如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$.
如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
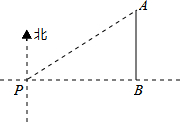 如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.
如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com