
分析 观察到每个分数分子均为1,分母是连续奇数,将第n个分数$\frac{1}{(2n-1)(2n+1)}$拆分成$\frac{1}{2}$×$(\frac{1}{2n-1}-\frac{1}{2n+1})$,然后提取公因数化简计算可得.
解答 解:原式=$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…+\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}×(1-\frac{1}{3})$+$\frac{1}{2}$×$(\frac{1}{3}-\frac{1}{5})$+$\frac{1}{2}×(\frac{1}{5}-\frac{1}{7})$+…+$\frac{1}{2}$×$(\frac{1}{2n-1}-\frac{1}{2n+1})$
=$\frac{1}{2}$×($1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n-1}-\frac{1}{2n+1}$)
=$\frac{1}{2}$×(1-$\frac{1}{2n+1}$)
=$\frac{n}{2n+1}$,
故答案为:$\frac{n}{2n+1}$.
点评 本题主要考查数字的变化类,从已知分数中寻求不变的量与变化的量及如何变化是总结规律的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
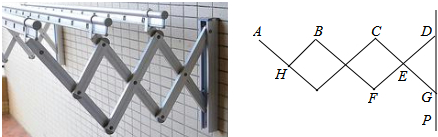
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
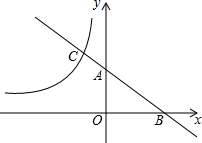 如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=-$\frac{3}{x}$的图象交于点C,若BA:AC=2:1,则a的值为( )
如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=-$\frac{3}{x}$的图象交于点C,若BA:AC=2:1,则a的值为( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
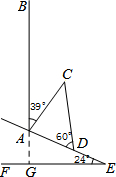 如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.
如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com