
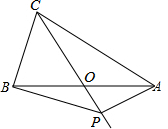
 如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$.
如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$. 分析 利用分类讨论,当∠APB=90°时,分两种情况讨论,情况一:如图1,易得∠PBA=30°,利用直角三角形斜边的中线等于斜边的一半得出结论;情况二:利用锐角三角函数得AP的长;如图2,当∠BAP=90°时,如图3,利用锐角三角函数得AP的长.
解答  解:当∠APB=90°时,分两种情况讨论,
解:当∠APB=90°时,分两种情况讨论,
情况一:如图1,
∵AO=BO,
∴PO=BO,
∵∠AOC=120°,
∴∠AOP=60°,
∴△AOP为等边三角形,
∴∠OAP=60°, ∴∠∠PBA=30°,
∴∠∠PBA=30°,
∴AP=$\frac{1}{2}$AB=2;
情况二:如图2,∵AO=BO,∠APB=90°,
∴PO=BO,
∵∠AOC=120°,
∴∠BOP=60°, ∴△BOP为等边三角形,
∴△BOP为等边三角形,
∴∠OBP=60°,
∴AP=AB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$;
当∠BAP=90°时,如图3,
∵∠AOC=120°,
∴∠AOP=60°,
∴AP=OA•tan∠AOP=2×$\sqrt{3}$=2$\sqrt{3}$.
故答案为:2或2$\sqrt{3}$.
点评 本题主要考查了勾股定理,含30°直角三角形的性质和直角三角形斜边的中线,利用分类讨论,数形结合是解答此题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
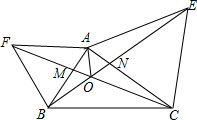 如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
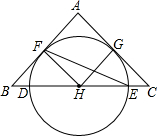 如图,在△ABC中,AB=AC,BC经过⊙H的圆心交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.
如图,在△ABC中,AB=AC,BC经过⊙H的圆心交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com