
分析 设每株月季花的价钱为x元,每株黄果兰的价钱为y元,根据钱数=单棵价钱×棵数,列出关于x、y的二元一次方程组,解出x、y的值,代入4x+2y中算出结果与100进行比较即可得出结论.
解答 解:设每株月季花的价钱为x元,每株黄果兰的价钱为y元,
根据题意得:$\left\{\begin{array}{l}{3x+4y=158}\\{2x+3y=117}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=35}\end{array}\right.$.
4x+2y=4×6+2×35=94(元),
94元<100元.
答:张老师用100元钱能买回他所需要的花卉.
点评 本题考查了二元一次方程组的应用,解题的关键:根据已知列出关于x、y的二元一次方程组.本题属于中档题,难度不大,在运算中利用解二元一次方程组求出x、y的值,再根据所要购买花卉的数量算出结果与100进行比较即可.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1<x2<x3 | B. | x3<x1<x2 | C. | x3<x2<x1 | D. | x2<x1<x3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
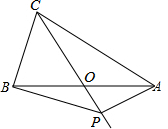 如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$.
如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
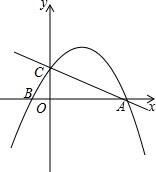 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
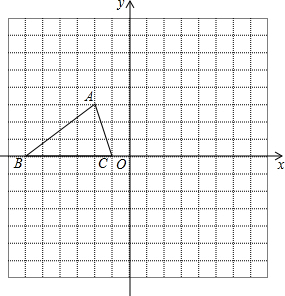 △ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上:
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
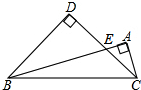 Rt△ABC中,∠ABC=15°,∠BAC=90°,以BC为斜边向A同侧作等腰直角△BDC交AB于E,若BC=$\sqrt{6}$,求S△BEC.
Rt△ABC中,∠ABC=15°,∠BAC=90°,以BC为斜边向A同侧作等腰直角△BDC交AB于E,若BC=$\sqrt{6}$,求S△BEC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com